Tight FPT Approximation for Constrained k-Center and k-Supplier
Paper and Code
Oct 27, 2021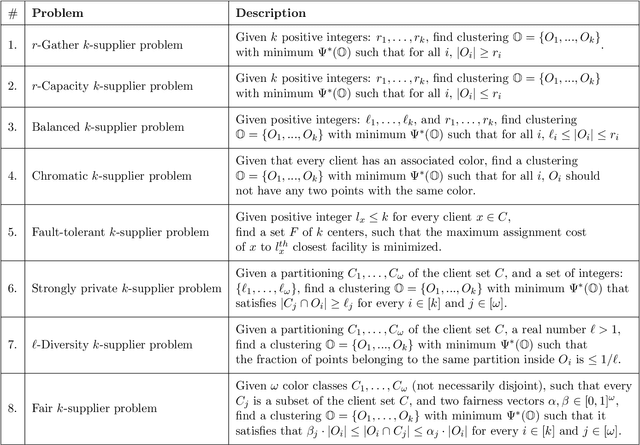
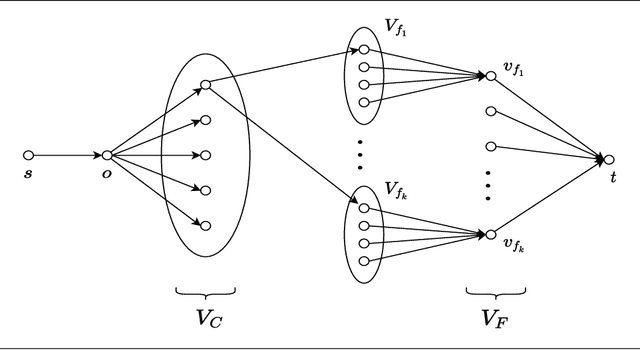
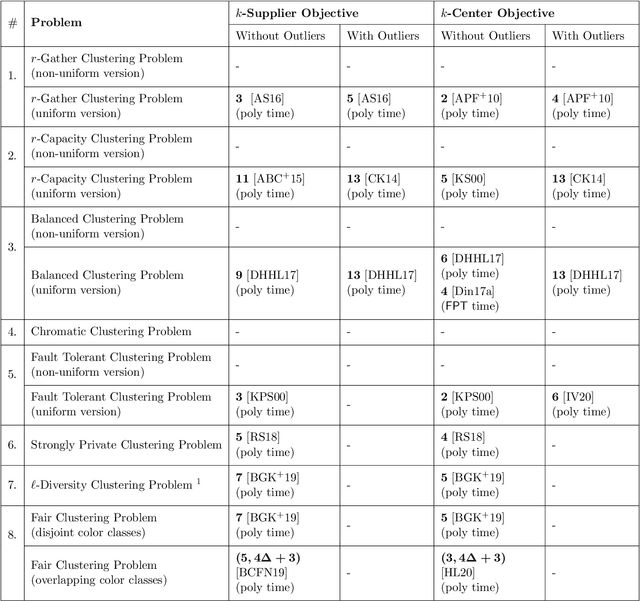
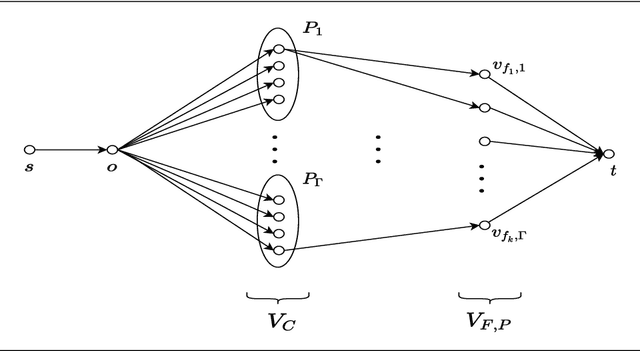
In this work, we study a range of constrained versions of the $k$-supplier and $k$-center problems such as: capacitated, fault-tolerant, fair, etc. These problems fall under a broad framework of constrained clustering. A unified framework for constrained clustering was proposed by Ding and Xu [SODA 2015] in context of the $k$-median and $k$-means objectives. In this work, we extend this framework to the $k$-supplier and $k$-center objectives. This unified framework allows us to obtain results simultaneously for the following constrained versions of the $k$-supplier problem: $r$-gather, $r$-capacity, balanced, chromatic, fault-tolerant, strongly private, $\ell$-diversity, and fair $k$-supplier problems, with and without outliers. We obtain the following results: We give $3$ and $2$ approximation algorithms for the constrained $k$-supplier and $k$-center problems, respectively, with $\mathsf{FPT}$ running time $k^{O(k)} \cdot n^{O(1)}$, where $n = |C \cup L|$. Moreover, these approximation guarantees are tight; that is, for any constant $\epsilon>0$, no algorithm can achieve $(3-\epsilon)$ and $(2-\epsilon)$ approximation guarantees for the constrained $k$-supplier and $k$-center problems in $\mathsf{FPT}$ time, assuming $\mathsf{FPT} \neq \mathsf{W}[2]$. Furthermore, we study these constrained problems in outlier setting. Our algorithm gives $3$ and $2$ approximation guarantees for the constrained outlier $k$-supplier and $k$-center problems, respectively, with $\mathsf{FPT}$ running time $(k+m)^{O(k)} \cdot n^{O(1)}$, where $n = |C \cup L|$ and $m$ is the number of outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge