Diego Colombo
A generalized back-door criterion
Jun 03, 2015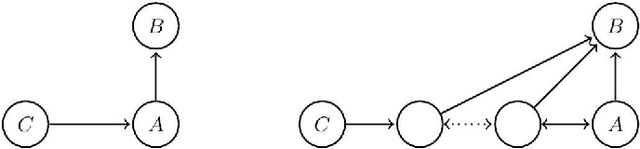
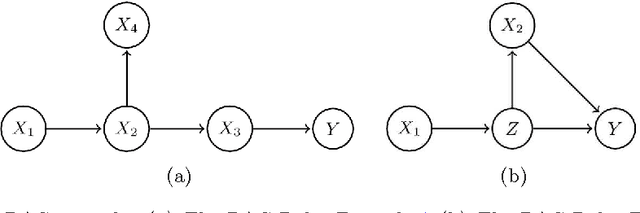
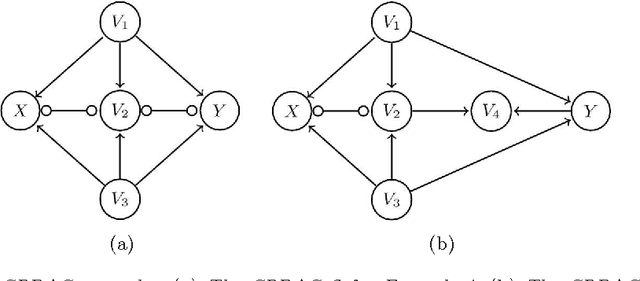
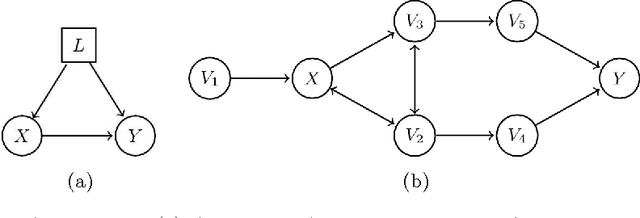
Abstract:We generalize Pearl's back-door criterion for directed acyclic graphs (DAGs) to more general types of graphs that describe Markov equivalence classes of DAGs and/or allow for arbitrarily many hidden variables. We also give easily checkable necessary and sufficient graphical criteria for the existence of a set of variables that satisfies our generalized back-door criterion, when considering a single intervention and a single outcome variable. Moreover, if such a set exists, we provide an explicit set that fulfills the criterion. We illustrate the results in several examples. R-code is available in the R-package pcalg.
* Published at http://dx.doi.org/10.1214/14-AOS1295 in the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
Order-independent constraint-based causal structure learning
Sep 27, 2013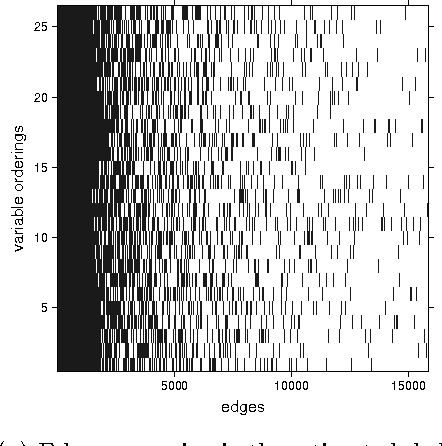
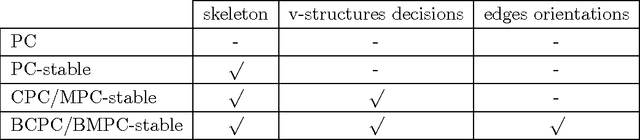
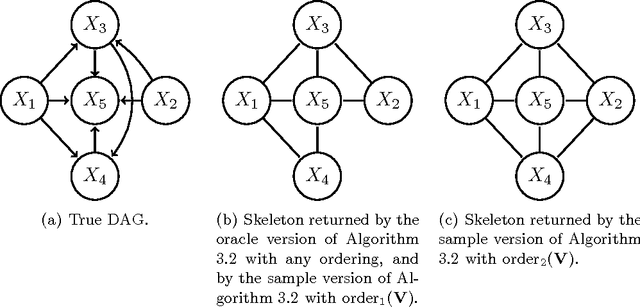

Abstract:We consider constraint-based methods for causal structure learning, such as the PC-, FCI-, RFCI- and CCD- algorithms (Spirtes et al. (2000, 1993), Richardson (1996), Colombo et al. (2012), Claassen et al. (2013)). The first step of all these algorithms consists of the PC-algorithm. This algorithm is known to be order-dependent, in the sense that the output can depend on the order in which the variables are given. This order-dependence is a minor issue in low-dimensional settings. We show, however, that it can be very pronounced in high-dimensional settings, where it can lead to highly variable results. We propose several modifications of the PC-algorithm (and hence also of the other algorithms) that remove part or all of this order-dependence. All proposed modifications are consistent in high-dimensional settings under the same conditions as their original counterparts. We compare the PC-, FCI-, and RFCI-algorithms and their modifications in simulation studies and on a yeast gene expression data set. We show that our modifications yield similar performance in low-dimensional settings and improved performance in high-dimensional settings. All software is implemented in the R-package pcalg.
Learning high-dimensional directed acyclic graphs with latent and selection variables
May 29, 2012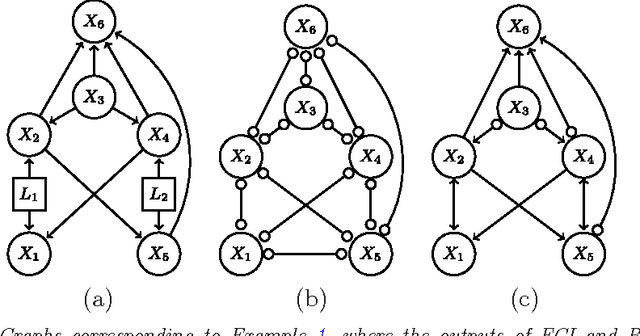
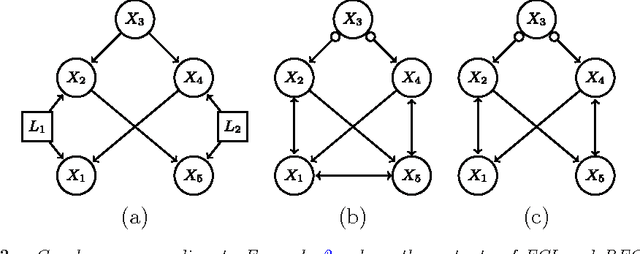
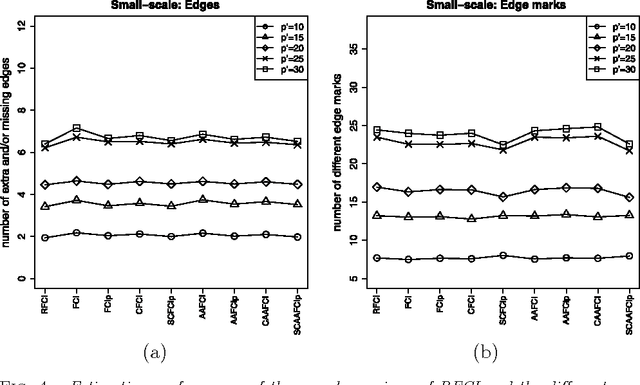
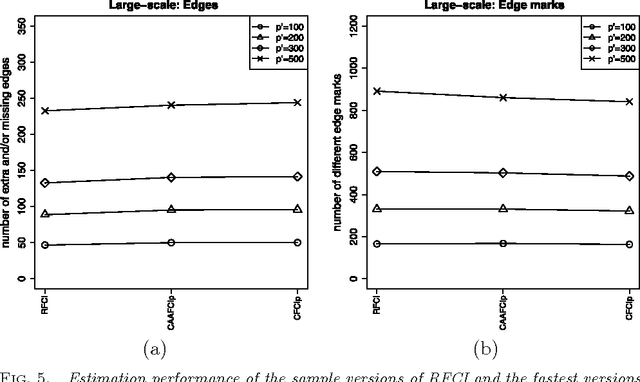
Abstract:We consider the problem of learning causal information between random variables in directed acyclic graphs (DAGs) when allowing arbitrarily many latent and selection variables. The FCI (Fast Causal Inference) algorithm has been explicitly designed to infer conditional independence and causal information in such settings. However, FCI is computationally infeasible for large graphs. We therefore propose the new RFCI algorithm, which is much faster than FCI. In some situations the output of RFCI is slightly less informative, in particular with respect to conditional independence information. However, we prove that any causal information in the output of RFCI is correct in the asymptotic limit. We also define a class of graphs on which the outputs of FCI and RFCI are identical. We prove consistency of FCI and RFCI in sparse high-dimensional settings, and demonstrate in simulations that the estimation performances of the algorithms are very similar. All software is implemented in the R-package pcalg.
* Published in at http://dx.doi.org/10.1214/11-AOS940 the Annals of Statistics (http://www.imstat.org/aos/) by the Institute of Mathematical Statistics (http://www.imstat.org)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge