Order-independent constraint-based causal structure learning
Paper and Code
Sep 27, 2013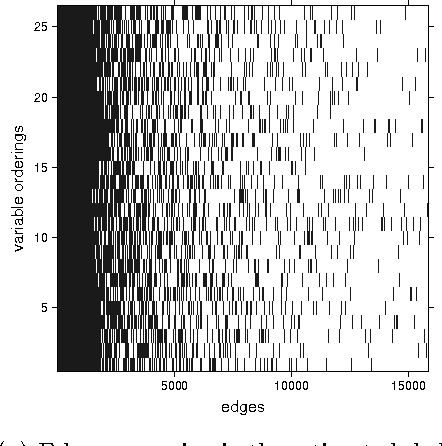
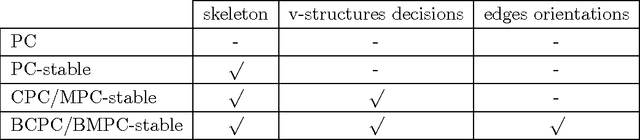
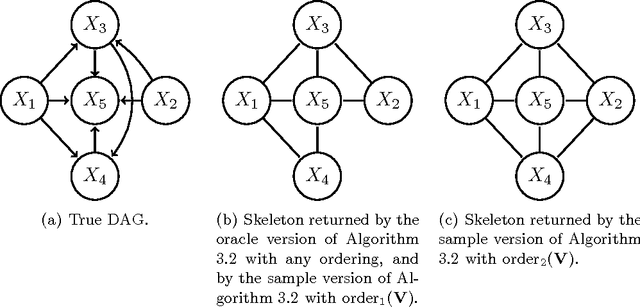

We consider constraint-based methods for causal structure learning, such as the PC-, FCI-, RFCI- and CCD- algorithms (Spirtes et al. (2000, 1993), Richardson (1996), Colombo et al. (2012), Claassen et al. (2013)). The first step of all these algorithms consists of the PC-algorithm. This algorithm is known to be order-dependent, in the sense that the output can depend on the order in which the variables are given. This order-dependence is a minor issue in low-dimensional settings. We show, however, that it can be very pronounced in high-dimensional settings, where it can lead to highly variable results. We propose several modifications of the PC-algorithm (and hence also of the other algorithms) that remove part or all of this order-dependence. All proposed modifications are consistent in high-dimensional settings under the same conditions as their original counterparts. We compare the PC-, FCI-, and RFCI-algorithms and their modifications in simulation studies and on a yeast gene expression data set. We show that our modifications yield similar performance in low-dimensional settings and improved performance in high-dimensional settings. All software is implemented in the R-package pcalg.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge