Devon R. Graham
Utilitarian Algorithm Configuration
Oct 31, 2023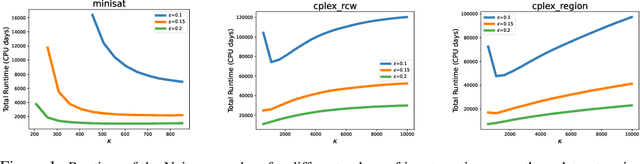

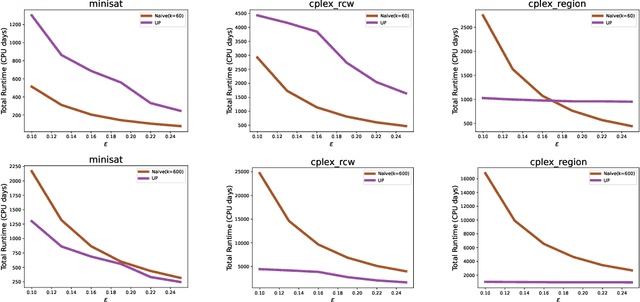
Abstract:We present the first nontrivial procedure for configuring heuristic algorithms to maximize the utility provided to their end users while also offering theoretical guarantees about performance. Existing procedures seek configurations that minimize expected runtime. However, very recent theoretical work argues that expected runtime minimization fails to capture algorithm designers' preferences. Here we show that the utilitarian objective also confers significant algorithmic benefits. Intuitively, this is because mean runtime is dominated by extremely long runs even when they are incredibly rare; indeed, even when an algorithm never gives rise to such long runs, configuration procedures that provably minimize mean runtime must perform a huge number of experiments to demonstrate this fact. In contrast, utility is bounded and monotonically decreasing in runtime, allowing for meaningful empirical bounds on a configuration's performance. This paper builds on this idea to describe effective and theoretically sound configuration procedures. We prove upper bounds on the runtime of these procedures that are similar to theoretical lower bounds, while also demonstrating their performance empirically.
Formalizing Preferences Over Runtime Distributions
May 25, 2022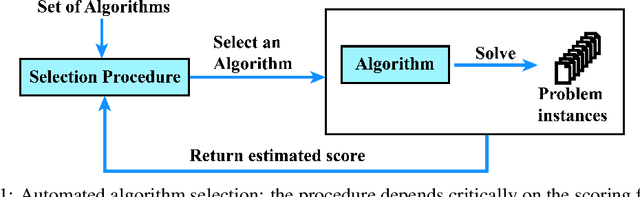
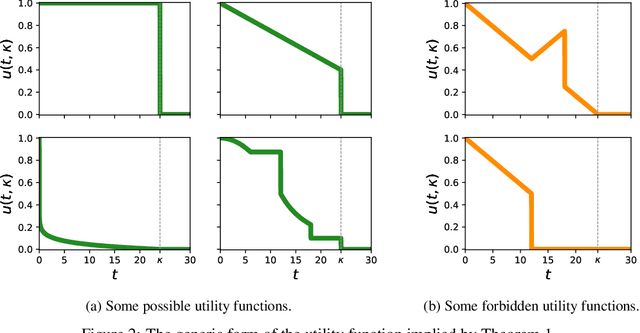
Abstract:When trying to solve a computational problem we are often faced with a choice among algorithms that are all guaranteed to return the right answer but that differ in their runtime distributions (e.g., SAT solvers, sorting algorithms). This paper aims to lay theoretical foundations for such choices by formalizing preferences over runtime distributions. It might seem that we should simply prefer the algorithm that minimizes expected runtime. However, such preferences would be driven by exactly how slow our algorithm is on bad inputs, whereas in practice we are typically willing to cut off occasional, sufficiently long runs before they finish. We propose a principled alternative, taking a utility-theoretic approach to characterize the scoring functions that describe preferences over algorithms. These functions depend on the way our value for solving our problem decreases with time and on the distribution from which captimes are drawn. We describe examples of realistic utility functions and show how to leverage a maximum-entropy approach for modeling underspecified captime distributions. Finally, we show how to efficiently estimate an algorithm's expected utility from runtime samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge