Desislava Bankova
Graded Entailment for Compositional Distributional Semantics
Jan 25, 2016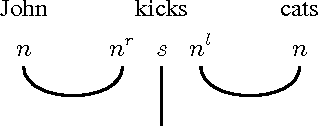
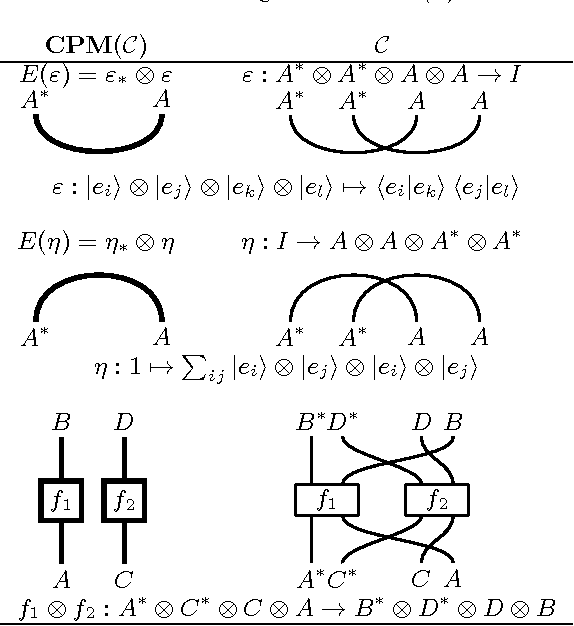
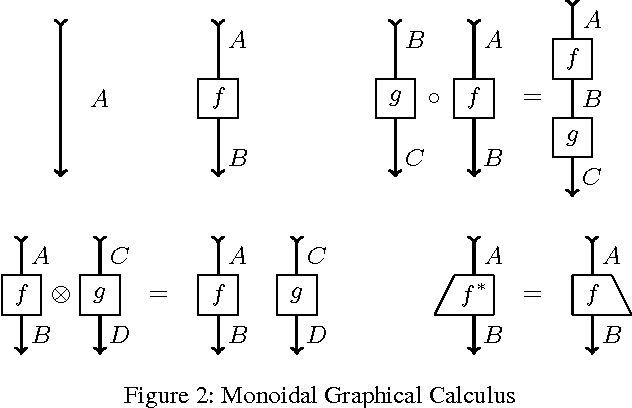
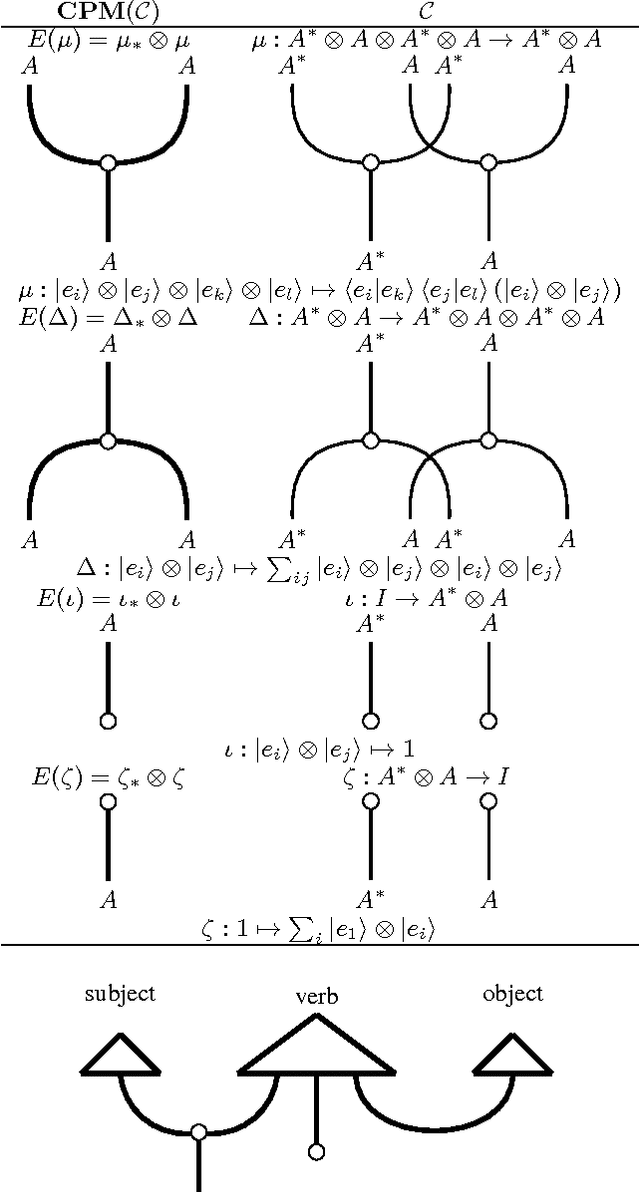
Abstract:The categorical compositional distributional model of natural language provides a conceptually motivated procedure to compute the meaning of sentences, given grammatical structure and the meanings of its words. This approach has outperformed other models in mainstream empirical language processing tasks. However, until recently it has lacked the crucial feature of lexical entailment -- as do other distributional models of meaning. In this paper we solve the problem of entailment for categorical compositional distributional semantics. Taking advantage of the abstract categorical framework allows us to vary our choice of model. This enables the introduction of a notion of entailment, exploiting ideas from the categorical semantics of partial knowledge in quantum computation. The new model of language uses density matrices, on which we introduce a novel robust graded order capturing the entailment strength between concepts. This graded measure emerges from a general framework for approximate entailment, induced by any commutative monoid. Quantum logic embeds in our graded order. Our main theorem shows that entailment strength lifts compositionally to the sentence level, giving a lower bound on sentence entailment. We describe the essential properties of graded entailment such as continuity, and provide a procedure for calculating entailment strength.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge