Data Augmentation with Variational Autoencoder for Imbalanced Dataset

Learning from an imbalanced distribution presents a major challenge in predictive modeling, as it generally leads to a reduction in the performance of standard algorithms. Various approaches exist to address this issue, but many of them concern classification problems, with a limited focus on regression. In this paper, we introduce a novel method aimed at enhancing learning on tabular data in the Imbalanced Regression (IR) framework, which remains a significant problem. We propose to use variational autoencoders (VAE) which are known as a powerful tool for synthetic data generation, offering an interesting approach to modeling and capturing latent representations of complex distributions. However, VAEs can be inefficient when dealing with IR. Therefore, we develop a novel approach for generating data, combining VAE with a smoothed bootstrap, specifically designed to address the challenges of IR. We numerically investigate the scope of this method by comparing it against its competitors on simulations and datasets known for IR.

Boarding for ISS: Imbalanced Self-Supervised: Discovery of a Scaled Autoencoder for Mixed Tabular Datasets

The field of imbalanced self-supervised learning, especially in the context of tabular data, has not been extensively studied. Existing research has predominantly focused on image datasets. This paper aims to fill this gap by examining the specific challenges posed by data imbalance in self-supervised learning in the domain of tabular data, with a primary focus on autoencoders. Autoencoders are widely employed for learning and constructing a new representation of a dataset, particularly for dimensionality reduction. They are also often used for generative model learning, as seen in variational autoencoders. When dealing with mixed tabular data, qualitative variables are often encoded using a one-hot encoder with a standard loss function (MSE or Cross Entropy). In this paper, we analyze the drawbacks of this approach, especially when categorical variables are imbalanced. We propose a novel metric to balance learning: a Multi-Supervised Balanced MSE. This approach reduces the reconstruction error by balancing the influence of variables. Finally, we empirically demonstrate that this new metric, compared to the standard MSE: i) outperforms when the dataset is imbalanced, especially when the learning process is insufficient, and ii) provides similar results in the opposite case.

Generalized Oversampling for Learning from Imbalanced datasets and Associated Theory

In supervised learning, it is quite frequent to be confronted with real imbalanced datasets. This situation leads to a learning difficulty for standard algorithms. Research and solutions in imbalanced learning have mainly focused on classification tasks. Despite its importance, very few solutions exist for imbalanced regression. In this paper, we propose a data augmentation procedure, the GOLIATH algorithm, based on kernel density estimates which can be used in classification and regression. This general approach encompasses two large families of synthetic oversampling: those based on perturbations, such as Gaussian Noise, and those based on interpolations, such as SMOTE. It also provides an explicit form of these machine learning algorithms and an expression of their conditional densities, in particular for SMOTE. New synthetic data generators are deduced. We apply GOLIATH in imbalanced regression combining such generator procedures with a wild-bootstrap resampling technique for the target values. We evaluate the performance of the GOLIATH algorithm in imbalanced regression situations. We empirically evaluate and compare our approach and demonstrate significant improvement over existing state-of-the-art techniques.

Data Augmentation for Imbalanced Regression

In this work, we consider the problem of imbalanced data in a regression framework when the imbalanced phenomenon concerns continuous or discrete covariates. Such a situation can lead to biases in the estimates. In this case, we propose a data augmentation algorithm that combines a weighted resampling (WR) and a data augmentation (DA) procedure. In a first step, the DA procedure permits exploring a wider support than the initial one. In a second step, the WR method drives the exogenous distribution to a target one. We discuss the choice of the DA procedure through a numerical study that illustrates the advantages of this approach. Finally, an actuarial application is studied.

Non-parametric Clustering of Multivariate Populations with Arbitrary Sizes

We propose a clustering procedure to group K populations into subgroups with the same dependence structure. The method is adapted to paired population and can be used with panel data. It relies on the differences between orthogonal projection coefficients of the K density copulas estimated from the K populations. Each cluster is then constituted by populations having significantly similar dependence structures. A recent test statistic from Ngounou-Bakam and Pommeret (2022) is used to construct automatically such clusters. The procedure is data driven and depends on the asymptotic level of the test. We illustrate our clustering algorithm via numerical studies and through two real datasets: a panel of financial datasets and insurance dataset of losses and allocated loss adjustment expense.

Mixed data Deep Gaussian Mixture Model: A clustering model for mixed datasets

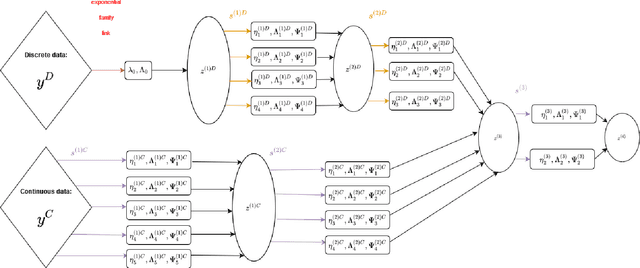
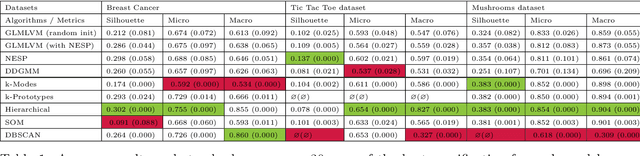
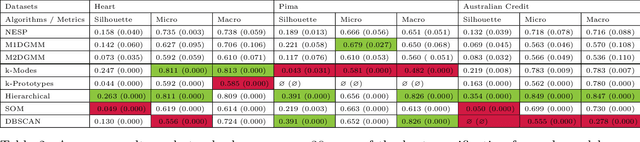
Clustering mixed data presents numerous challenges inherent to the very heterogeneous nature of the variables. Two major difficulties lie in the initialisation of the algorithms and in making variables comparable between types. This work is concerned with these two problems. We introduce a two-heads architecture model-based clustering method called Mixed data Deep Gaussian Mixture Model (MDGMM) that can be viewed as an automatic way to merge the clusterings performed separately on continuous and non continuous data. We also design a new initialisation strategy and a data driven method that selects "on the fly" the best specification of the model and the optimal number of clusters for a given dataset. Besides, our model provides continuous low-dimensional representations of the data which can be a useful tool to visualize mixed datasets. Finally, we validate the performance of our approach comparing its results with state-of-the-art mixed data clustering models over several commonly used datasets