LOCUS: A Distribution-Free Loss-Quantile Score for Risk-Aware Predictions

Modern machine learning models can be accurate on average yet still make mistakes that dominate deployment cost. We introduce Locus, a distribution-free wrapper that produces a per-input loss-scale reliability score for a fixed prediction function. Rather than quantifying uncertainty about the label, Locus models the realized loss of the prediction function using any engine that outputs a predictive distribution for the loss given an input. A simple split-calibration step turns this function into a distribution-free interpretable score that is comparable across inputs and can be read as an upper loss level. The score is useful on its own for ranking, and it can optionally be thresholded to obtain a transparent flagging rule with distribution-free control of large-loss events. Experiments across 13 regression benchmarks show that Locus yields effective risk ranking and reduces large-loss frequency compared to standard heuristics.

A new LDA formulation with covariates

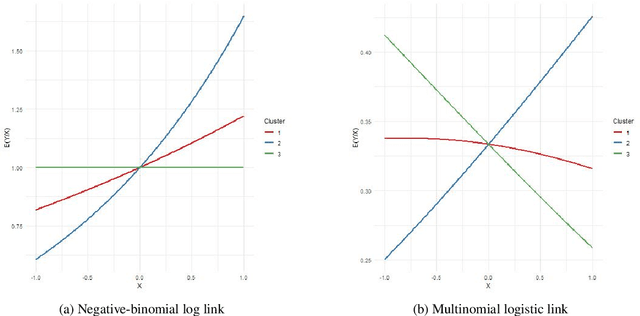
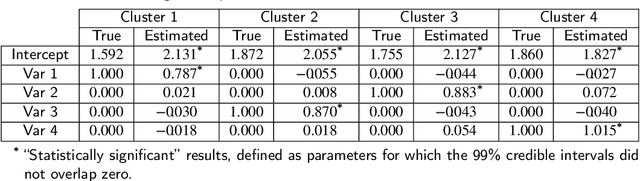
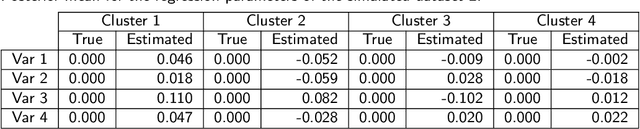
The Latent Dirichlet Allocation (LDA) model is a popular method for creating mixed-membership clusters. Despite having been originally developed for text analysis, LDA has been used for a wide range of other applications. We propose a new formulation for the LDA model which incorporates covariates. In this model, a negative binomial regression is embedded within LDA, enabling straight-forward interpretation of the regression coefficients and the analysis of the quantity of cluster-specific elements in each sampling units (instead of the analysis being focused on modeling the proportion of each cluster, as in Structural Topic Models). We use slice sampling within a Gibbs sampling algorithm to estimate model parameters. We rely on simulations to show how our algorithm is able to successfully retrieve the true parameter values and the ability to make predictions for the abundance matrix using the information given by the covariates. The model is illustrated using real data sets from three different areas: text-mining of Coronavirus articles, analysis of grocery shopping baskets, and ecology of tree species on Barro Colorado Island (Panama). This model allows the identification of mixed-membership clusters in discrete data and provides inference on the relationship between covariates and the abundance of these clusters.