Denis Efimov
NON-A-POST
Learning linear dynamical systems under convex constraints
Mar 27, 2023Abstract:We consider the problem of identification of linear dynamical systems from a single trajectory. Recent results have predominantly focused on the setup where no structural assumption is made on the system matrix $A^* \in \mathbb{R}^{n \times n}$, and have consequently analyzed the ordinary least squares (OLS) estimator in detail. We assume prior structural information on $A^*$ is available, which can be captured in the form of a convex set $\mathcal{K}$ containing $A^*$. For the solution of the ensuing constrained least squares estimator, we derive non-asymptotic error bounds in the Frobenius norm which depend on the local size of the tangent cone of $\mathcal{K}$ at $A^*$. To illustrate the usefulness of this result, we instantiate it for the settings where, (i) $\mathcal{K}$ is a $d$ dimensional subspace of $\mathbb{R}^{n \times n}$, or (ii) $A^*$ is $k$-sparse and $\mathcal{K}$ is a suitably scaled $\ell_1$ ball. In the regimes where $d, k \ll n^2$, our bounds improve upon those obtained from the OLS estimator.
Robust Estimation, Prediction and Control with Linear Dynamics and Generic Costs
Feb 25, 2020
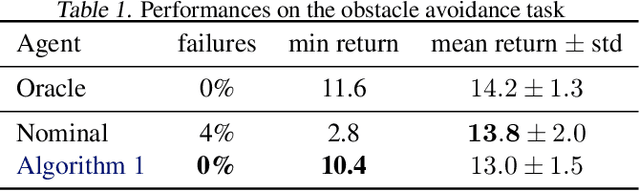


Abstract:We develop a framework for the adaptive model predictive control of a linear system with unknown parameters and arbitrary bounded costs, in a critical setting where failures are costly and should be prevented at all time. Our approach builds on two ideas: first, we incorporate prior knowledge of the dynamics in the form of a known structure that shapes uncertainty, which can be tightened as we collect interaction data by building high-confidence regions through least-square regression. Second, in order to handle this uncertainty we formulate a robust control objective. Leveraging tools from the interval prediction literature, we convert the confidence regions on parameters into confidence sets on trajectories induced by the controls. These controls are then optimised resorting to tree-based planning methods. We eventually relax our modeling assumptions with a multi-model extension based on a data-driven robust model selection mechanism. The full procedure is designed to produce reasonable and safe behaviours at deployment while recovering an asymptotic optimality. We illustrate it on a practical case of autonomous driving at a crossroads intersection among vehicles with uncertain behaviours.
Approximate Robust Control of Uncertain Dynamical Systems
Mar 01, 2019


Abstract:This work studies the design of safe control policies for large-scale non-linear systems operating in uncertain environments. In such a case, the robust control framework is a principled approach to safety that aims to maximize the worst-case performance of a system. However, the resulting optimization problem is generally intractable for non-linear systems with continuous states. To overcome this issue, we introduce two tractable methods that are based either on sampling or on a conservative approximation of the robust objective. The proposed approaches are applied to the problem of autonomous driving.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge