Robust Estimation, Prediction and Control with Linear Dynamics and Generic Costs

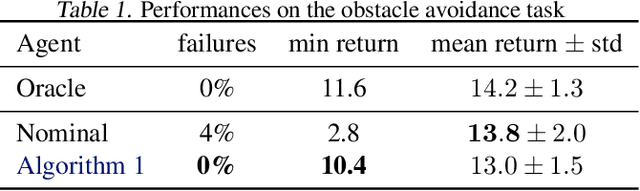
We develop a framework for the adaptive model predictive control of a linear system with unknown parameters and arbitrary bounded costs, in a critical setting where failures are costly and should be prevented at all time. Our approach builds on two ideas: first, we incorporate prior knowledge of the dynamics in the form of a known structure that shapes uncertainty, which can be tightened as we collect interaction data by building high-confidence regions through least-square regression. Second, in order to handle this uncertainty we formulate a robust control objective. Leveraging tools from the interval prediction literature, we convert the confidence regions on parameters into confidence sets on trajectories induced by the controls. These controls are then optimised resorting to tree-based planning methods. We eventually relax our modeling assumptions with a multi-model extension based on a data-driven robust model selection mechanism. The full procedure is designed to produce reasonable and safe behaviours at deployment while recovering an asymptotic optimality. We illustrate it on a practical case of autonomous driving at a crossroads intersection among vehicles with uncertain behaviours.