David Martinez Rego
Jacobian Regularization for Mitigating Universal Adversarial Perturbations
Apr 21, 2021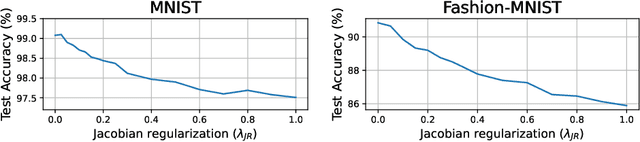
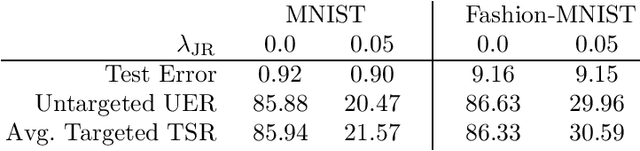
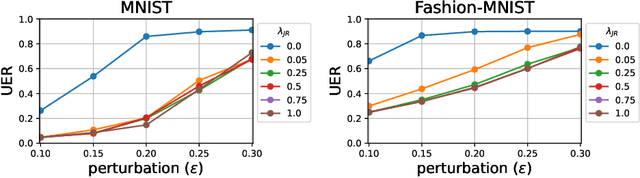
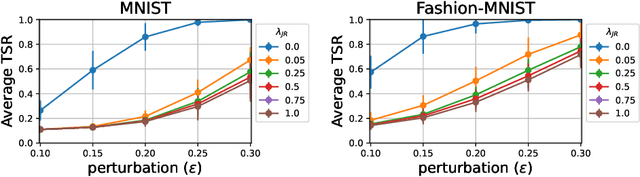
Abstract:Universal Adversarial Perturbations (UAPs) are input perturbations that can fool a neural network on large sets of data. They are a class of attacks that represents a significant threat as they facilitate realistic, practical, and low-cost attacks on neural networks. In this work, we derive upper bounds for the effectiveness of UAPs based on norms of data-dependent Jacobians. We empirically verify that Jacobian regularization greatly increases model robustness to UAPs by up to four times whilst maintaining clean performance. Our theoretical analysis also allows us to formulate a metric for the strength of shared adversarial perturbations between pairs of inputs. We apply this metric to benchmark datasets and show that it is highly correlated with the actual observed robustness. This suggests that realistic and practical universal attacks can be reliably mitigated without sacrificing clean accuracy, which shows promise for the robustness of machine learning systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge