Online Dynamic Pricing for Electric Vehicle Charging Stations with Reservations

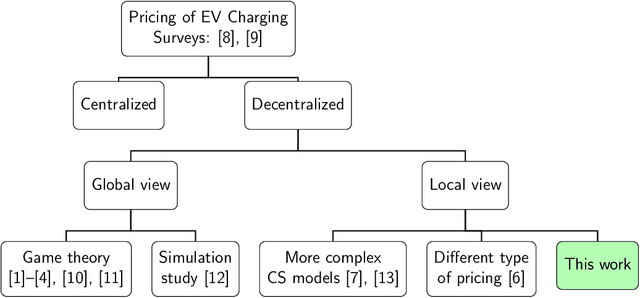
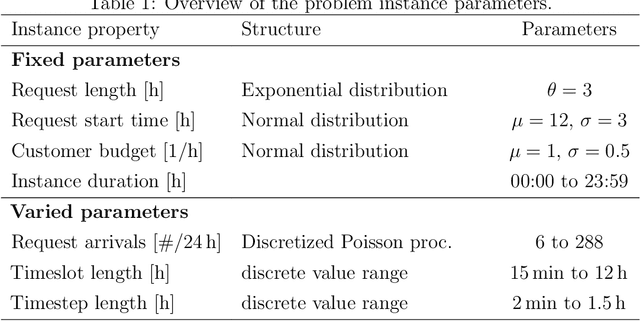
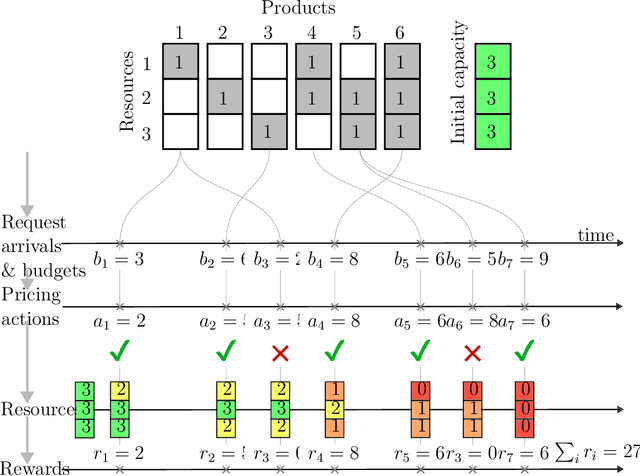
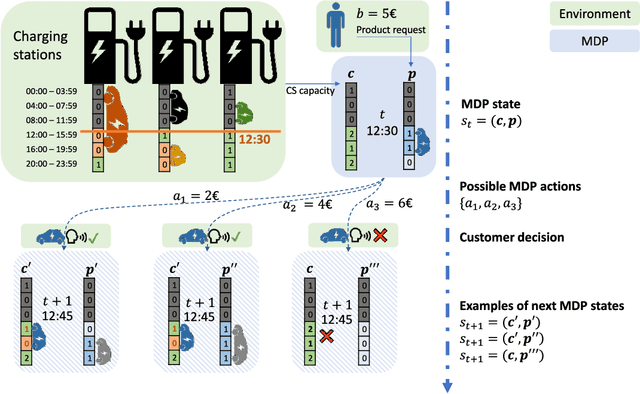
The transition to electric vehicles (EVs), coupled with the rise of renewable energy sources, will significantly impact the electric grid. Unlike conventional fuel sources, electricity for EVs is constrained by grid capacity, price fluctuations, and long EV charging times, requiring new pricing solutions to manage demand and supply. This paper proposes a model for online dynamic pricing of reserved EV charging services, including reservation, parking, and charging as a bundled service priced as a whole. Our approach focuses on the individual charging station operator, employing a stochastic demand model and online dynamic pricing based on expected demand. The proposed model uses a Markov Decision Process (MDP) formulation to optimize sequential pricing decisions for charging session requests. A key contribution is the novel definition and quantification of discretization error introduced by the discretization of the Poisson process for use in the MDP. The model's viability is demonstrated with a heuristic solution method based on Monte-Carlo tree search, offering a viable path for real-world application.

Optimal Chaining of Vehicle Plans with Time Windows

For solving problems from the domain of Mobility-on-Demand (MoD), we often need to connect vehicle plans into plans spanning longer time, a process we call plan chaining. As we show in this work, chaining of the plans can be used to reduce the size of MoD providers' fleet (fleet-sizing problem) but also to reduce the total driven distance by providing high-quality vehicle dispatching solutions in MoD systems. Recently, a solution that uses this principle has been proposed to solve the fleet-sizing problem. The method does not consider the time flexibility of the plans. Instead, plans are fixed in time and cannot be delayed. However, time flexibility is an essential property of all vehicle problems with time windows. This work presents a new plan chaining formulation that considers delays as allowed by the time windows and a solution method for solving it. Moreover, we prove that the proposed plan chaining method is optimal, and we analyze its complexity. Finally, we list some practical applications and perform a demonstration for one of them: a new heuristic vehicle dispatching method for solving the static dial-a-ride problem. The demonstration results show that our proposed method provides a better solution than the two heuristic baselines for the majority of instances that cannot be solved optimally. At the same time, our method does not have the largest computational time requirements compared to the baselines. Therefore, we conclude that the proposed optimal chaining method provides not only theoretically sound results but is also practically applicable.

Large-scale Ridesharing DARP Instances Based on Real Travel Demand

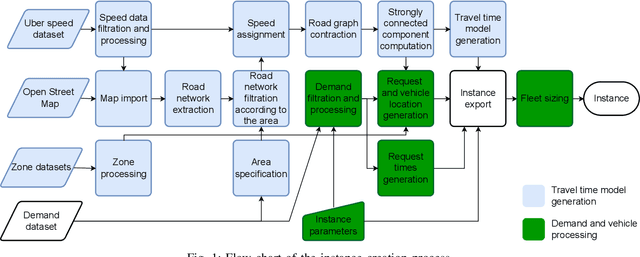
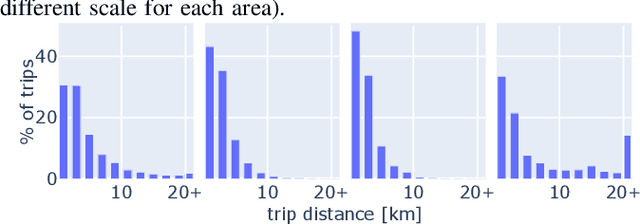
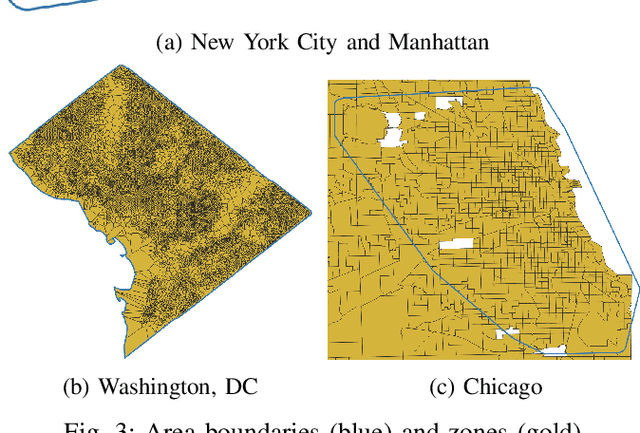
Accurately predicting the real-life performance of algorithms solving the Dial-a-Ride Problem (DARP) in the context of Mobility on Demand (MoD) systems with ridesharing requires evaluating them on representative instances. However, the benchmarking of state-of-the-art DARP solution methods has been limited to small, artificial instances or outdated non-public instances, hindering direct comparisons. With the rise of large MoD systems and the availability of open travel demand datasets for many US cities, there is now an opportunity to evaluate these algorithms on standardized, realistic, and representative instances. Despite the significant challenges involved in processing obfuscated and diverse datasets, we have developed a methodology using which we have created a comprehensive set of large-scale demand instances based on real-world data. These instances cover diverse use cases, one of which is demonstrated in an evaluation of two established DARP methods: the insertion heuristic and optimal vehicle-group assignment method. We publish the full results of both methods in a standardized format. The results show significant differences between areas in all measured quantities, emphasizing the importance of evaluating methods across different cities.

Map Matching Algorithm for Large-scale Datasets

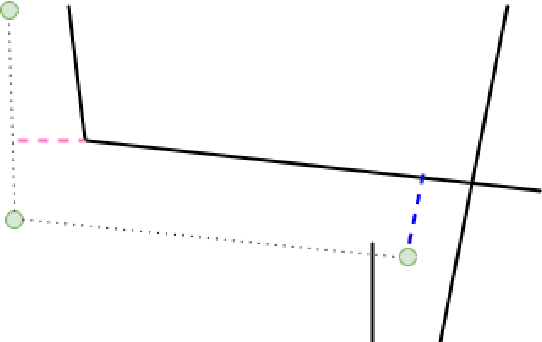
GPS receivers embedded in cell phones and connected vehicles generate a series of location measurements that can be used for various analytical purposes. A common pre-processing step of this data is the so-called map matching. The goal of map matching is to infer the trajectory that the device followed in a road network from a potentially sparse series of noisy location measurements. Although accurate and robust map matching algorithms based on probabilistic models exist, they are computationally heavy and thus impractical for processing of large datasets. In this paper, we present a scalable map-matching algorithm based on Dijkstra shortest path method, that is both accurate and applicable to large datasets. Our experiments on a publicly-available dataset showed that the proposed method achieves accuracy that is comparable to that of the existing map matching methods using only a fraction of computational resources. In result, our algorithm can be used to efficiently process large datasets of noisy and potentially sparse location data that would be unexploitable using existing techniques due to their high computational requirements.