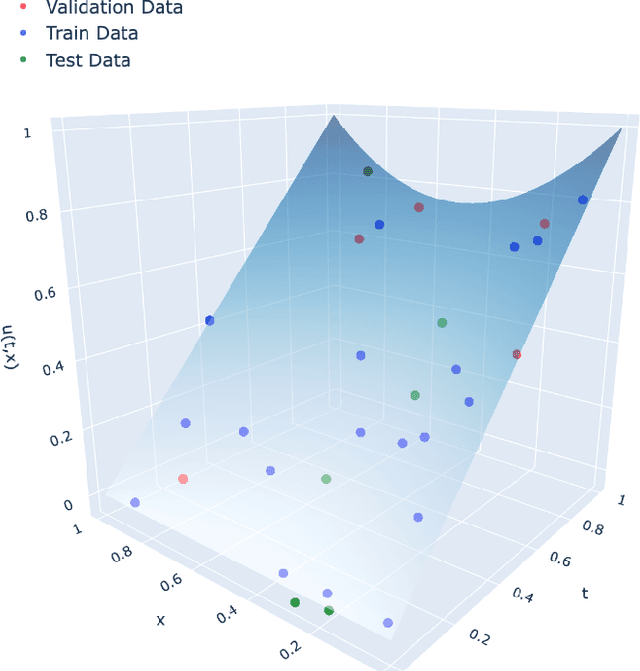
MonoKAN: Certified Monotonic Kolmogorov-Arnold Network

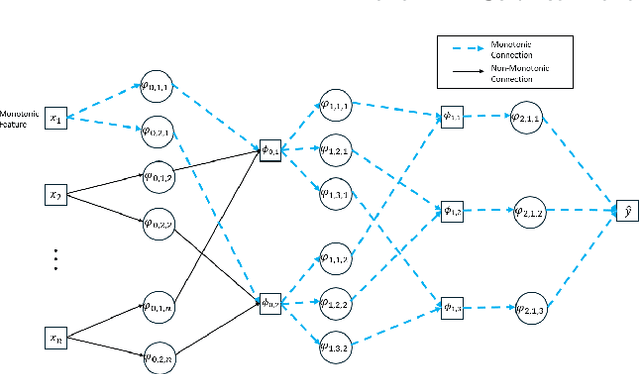
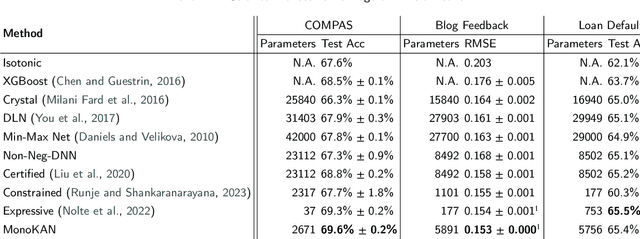
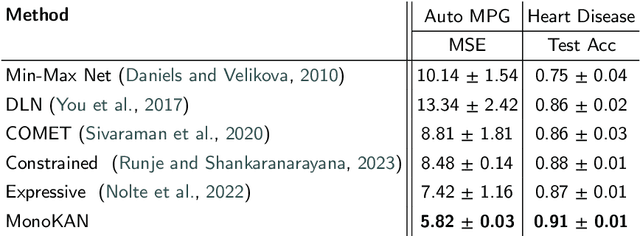
Artificial Neural Networks (ANNs) have significantly advanced various fields by effectively recognizing patterns and solving complex problems. Despite these advancements, their interpretability remains a critical challenge, especially in applications where transparency and accountability are essential. To address this, explainable AI (XAI) has made progress in demystifying ANNs, yet interpretability alone is often insufficient. In certain applications, model predictions must align with expert-imposed requirements, sometimes exemplified by partial monotonicity constraints. While monotonic approaches are found in the literature for traditional Multi-layer Perceptrons (MLPs), they still face difficulties in achieving both interpretability and certified partial monotonicity. Recently, the Kolmogorov-Arnold Network (KAN) architecture, based on learnable activation functions parametrized as splines, has been proposed as a more interpretable alternative to MLPs. Building on this, we introduce a novel ANN architecture called MonoKAN, which is based on the KAN architecture and achieves certified partial monotonicity while enhancing interpretability. To achieve this, we employ cubic Hermite splines, which guarantee monotonicity through a set of straightforward conditions. Additionally, by using positive weights in the linear combinations of these splines, we ensure that the network preserves the monotonic relationships between input and output. Our experiments demonstrate that MonoKAN not only enhances interpretability but also improves predictive performance across the majority of benchmarks, outperforming state-of-the-art monotonic MLP approaches.

A Mathematical Certification for Positivity Conditions in Neural Networks with Applications to Partial Monotonicity and Ethical AI

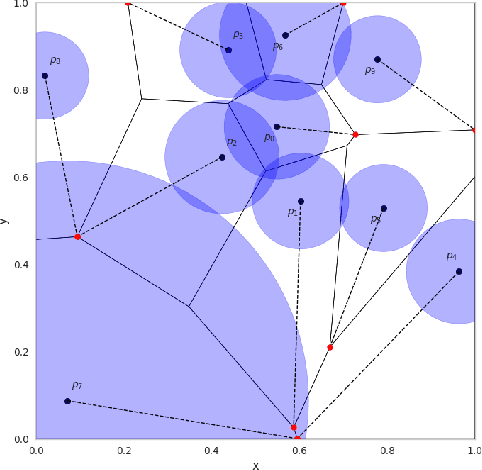
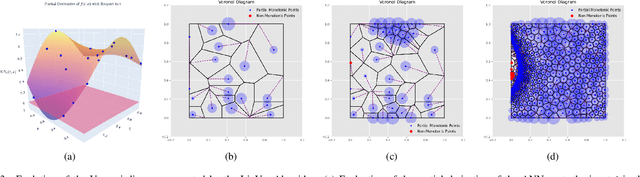
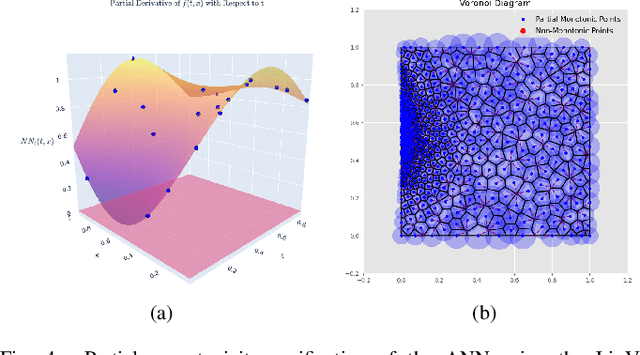
Artificial Neural Networks (ANNs) have become a powerful tool for modeling complex relationships in large-scale datasets. However, their black-box nature poses ethical challenges. In certain situations, ensuring ethical predictions might require following specific partial monotonic constraints. However, certifying if an already-trained ANN is partially monotonic is challenging. Therefore, ANNs are often disregarded in some critical applications, such as credit scoring, where partial monotonicity is required. To address this challenge, this paper presents a novel algorithm (LipVor) that certifies if a black-box model, such as an ANN, is positive based on a finite number of evaluations. Therefore, as partial monotonicity can be stated as a positivity condition of the partial derivatives, the LipVor Algorithm can certify whether an already trained ANN is partially monotonic. To do so, for every positively evaluated point, the Lipschitzianity of the black-box model is used to construct a specific neighborhood where the function remains positive. Next, based on the Voronoi diagram of the evaluated points, a sufficient condition is stated to certify if the function is positive in the domain. Compared to prior methods, our approach is able to mathematically certify if an ANN is partially monotonic without needing constrained ANN's architectures or piece-wise linear activation functions. Therefore, LipVor could open up the possibility of using unconstrained ANN in some critical fields. Moreover, some other properties of an ANN, such as convexity, can be posed as positivity conditions, and therefore, LipVor could also be applied.

Metric Tools for Sensitivity Analysis with Applications to Neural Networks

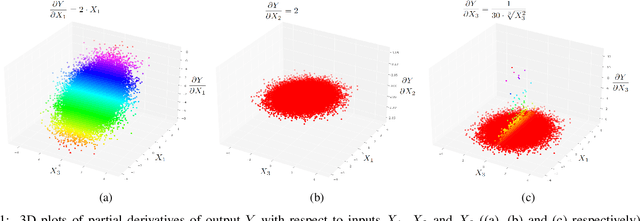
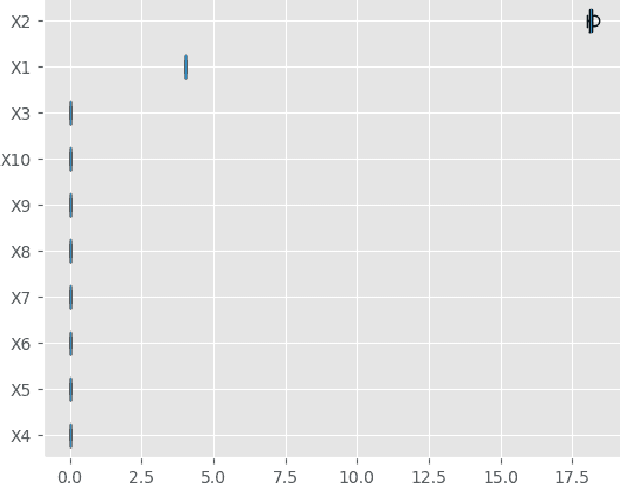
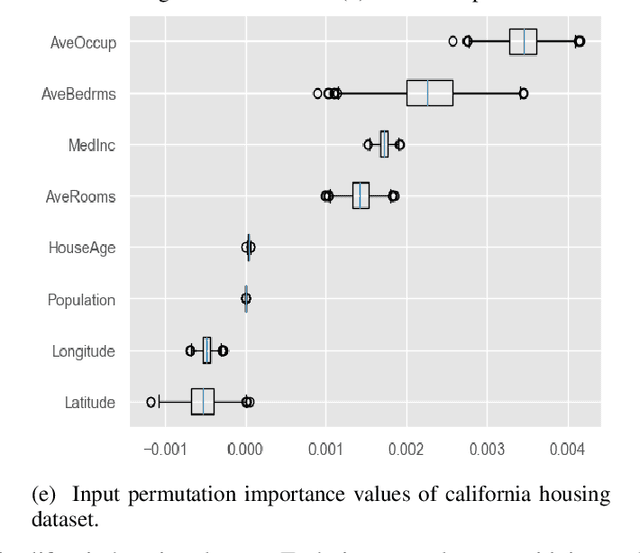
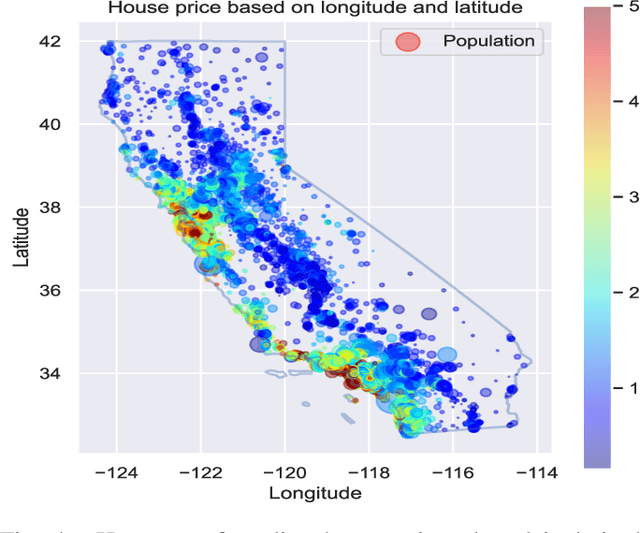
As Machine Learning models are considered for autonomous decisions with significant social impact, the need for understanding how these models work rises rapidly. Explainable Artificial Intelligence (XAI) aims to provide interpretations for predictions made by Machine Learning models, in order to make the model trustworthy and more transparent for the user. For example, selecting relevant input variables for the problem directly impacts the model's ability to learn and make accurate predictions, so obtaining information about input importance play a crucial role when training the model. One of the main XAI techniques to obtain input variable importance is the sensitivity analysis based on partial derivatives. However, existing literature of this method provide no justification of the aggregation metrics used to retrieved information from the partial derivatives. In this paper, a theoretical framework is proposed to study sensitivities of ML models using metric techniques. From this metric interpretation, a complete family of new quantitative metrics called $\alpha$-curves is extracted. These $\alpha$-curves provide information with greater depth on the importance of the input variables for a machine learning model than existing XAI methods in the literature. We demonstrate the effectiveness of the $\alpha$-curves using synthetic and real datasets, comparing the results against other XAI methods for variable importance and validating the analysis results with the ground truth or literature information.