A Mathematical Certification for Positivity Conditions in Neural Networks with Applications to Partial Monotonicity and Ethical AI

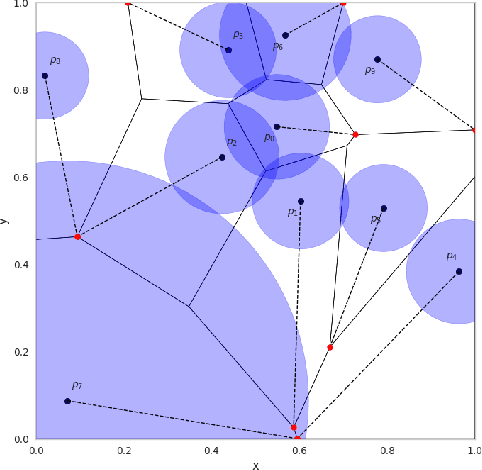
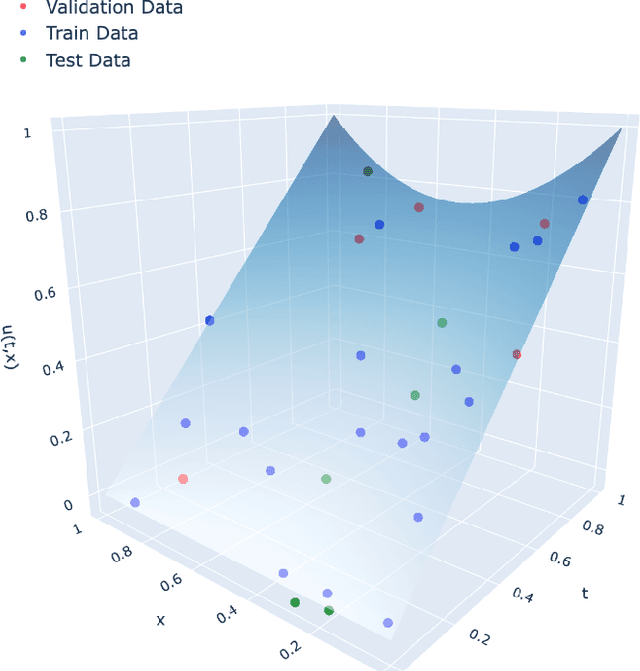
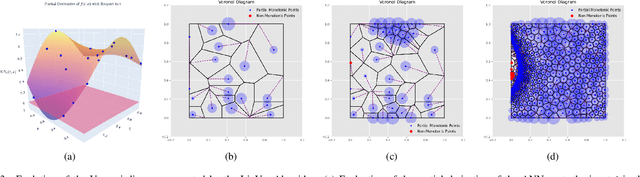
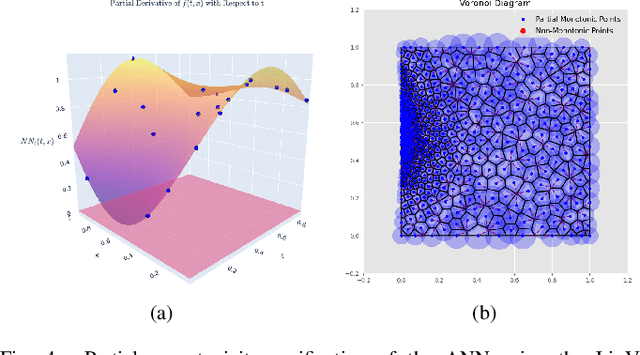
Artificial Neural Networks (ANNs) have become a powerful tool for modeling complex relationships in large-scale datasets. However, their black-box nature poses ethical challenges. In certain situations, ensuring ethical predictions might require following specific partial monotonic constraints. However, certifying if an already-trained ANN is partially monotonic is challenging. Therefore, ANNs are often disregarded in some critical applications, such as credit scoring, where partial monotonicity is required. To address this challenge, this paper presents a novel algorithm (LipVor) that certifies if a black-box model, such as an ANN, is positive based on a finite number of evaluations. Therefore, as partial monotonicity can be stated as a positivity condition of the partial derivatives, the LipVor Algorithm can certify whether an already trained ANN is partially monotonic. To do so, for every positively evaluated point, the Lipschitzianity of the black-box model is used to construct a specific neighborhood where the function remains positive. Next, based on the Voronoi diagram of the evaluated points, a sufficient condition is stated to certify if the function is positive in the domain. Compared to prior methods, our approach is able to mathematically certify if an ANN is partially monotonic without needing constrained ANN's architectures or piece-wise linear activation functions. Therefore, LipVor could open up the possibility of using unconstrained ANN in some critical fields. Moreover, some other properties of an ANN, such as convexity, can be posed as positivity conditions, and therefore, LipVor could also be applied.