Marimba: A Tool for Verifying Properties of Hidden Markov Models

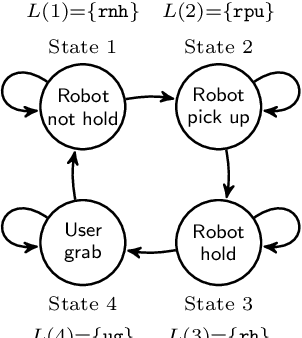
The formal verification of properties of Hidden Markov Models (HMMs) is highly desirable for gaining confidence in the correctness of the model and the corresponding system. A significant step towards HMM verification was the development by Zhang et al. of a family of logics for verifying HMMs, called POCTL*, and its model checking algorithm. As far as we know, the verification tool we present here is the first one based on Zhang et al.'s approach. As an example of its effective application, we verify properties of a handover task in the context of human-robot interaction. Our tool was implemented in Haskell, and the experimental evaluation was performed using the humanoid robot Bert2.

The Dynamically Extended Mind -- A Minimal Modeling Case Study

The extended mind hypothesis has stimulated much interest in cognitive science. However, its core claim, i.e. that the process of cognition can extend beyond the brain via the body and into the environment, has been heavily criticized. A prominent critique of this claim holds that when some part of the world is coupled to a cognitive system this does not necessarily entail that the part is also constitutive of that cognitive system. This critique is known as the "coupling-constitution fallacy". In this paper we respond to this reductionist challenge by using an evolutionary robotics approach to create a minimal model of two acoustically coupled agents. We demonstrate how the interaction process as a whole has properties that cannot be reduced to the contributions of the isolated agents. We also show that the neural dynamics of the coupled agents has formal properties that are inherently impossible for those neural networks in isolation. By keeping the complexity of the model to an absolute minimum, we are able to illustrate how the coupling-constitution fallacy is in fact based on an inadequate understanding of the constitutive role of nonlinear interactions in dynamical systems theory.

Self-organizing traffic lights at multiple-street intersections

Summary: Traffic light coordination is a complex problem. In this paper, we extend previous work on an abstract model of city traffic to allow for multiple street intersections. We test a self-organizing method in our model, showing that it is close to theoretical optima and superior to a traditional method of traffic light coordination. Abstract: The elementary cellular automaton following rule 184 can mimic particles flowing in one direction at a constant speed. This automaton can therefore model highway traffic. In a recent paper, we have incorporated intersections regulated by traffic lights to this model using exclusively elementary cellular automata. In such a paper, however, we only explored a rectangular grid. We now extend our model to more complex scenarios employing an hexagonal grid. This extension shows first that our model can readily incorporate multiple-way intersections and hence simulate complex scenarios. In addition, the current extension allows us to study and evaluate the behavior of two different kinds of traffic light controller for a grid of six-way streets allowing for either two or three street intersections: a traffic light that tries to adapt to the amount of traffic (which results in self-organizing traffic lights) and a system of synchronized traffic lights with coordinated rigid periods (sometimes called the "green wave" method). We observe a tradeoff between system capacity and topological complexity. The green wave method is unable to cope with the complexity of a higher-capacity scenario, while the self-organizing method is scalable, adapting to the complexity of a scenario and exploiting its maximum capacity. Additionally, in this paper we propose a benchmark, independent of methods and models, to measure the performance of a traffic light controller comparing it against a theoretical optimum.

Modeling self-organizing traffic lights with elementary cellular automata

There have been several highway traffic models proposed based on cellular automata. The simplest one is elementary cellular automaton rule 184. We extend this model to city traffic with cellular automata coupled at intersections using only rules 184, 252, and 136. The simplicity of the model offers a clear understanding of the main properties of city traffic and its phase transitions. We use the proposed model to compare two methods for coordinating traffic lights: a green-wave method that tries to optimize phases according to expected flows and a self-organizing method that adapts to the current traffic conditions. The self-organizing method delivers considerable improvements over the green-wave method. For low densities, the self-organizing method promotes the formation and coordination of platoons that flow freely in four directions, i.e. with a maximum velocity and no stops. For medium densities, the method allows a constant usage of the intersections, exploiting their maximum flux capacity. For high densities, the method prevents gridlocks and promotes the formation and coordination of "free-spaces" that flow in the opposite direction of traffic.