Darshan Bryner
Diagnosing Generalization Failures in Fine-Tuned LLMs: A Cross-Architectural Study on Phishing Detection
Jan 15, 2026Abstract:The practice of fine-tuning Large Language Models (LLMs) has achieved state-of-the-art performance on specialized tasks, yet diagnosing why these models become brittle and fail to generalize remains a critical open problem. To address this, we introduce and apply a multi-layered diagnostic framework to a cross-architectural study. We fine-tune Llama 3.1 8B, Gemma 2 9B, and Mistral models on a high-stakes phishing detection task and use SHAP analysis and mechanistic interpretability to uncover the root causes of their generalization failures. Our investigation reveals three critical findings: (1) Generalization is driven by a powerful synergy between architecture and data diversity. The Gemma 2 9B model achieves state-of-the-art performance (>91\% F1), but only when trained on a stylistically diverse ``generalist'' dataset. (2) Generalization is highly architecture-dependent. We diagnose a specific failure mode in Llama 3.1 8B, which performs well on a narrow domain but cannot integrate diverse data, leading to a significant performance drop. (3) Some architectures are inherently more generalizable. The Mistral model proves to be a consistent and resilient performer across multiple training paradigms. By pinpointing the flawed heuristics responsible for these failures, our work provides a concrete methodology for diagnosing and understanding generalization failures, underscoring that reliable AI requires deep validation of the interplay between architecture, data, and training strategy.
Shape Analysis of Functional Data with Elastic Partial Matching
May 18, 2021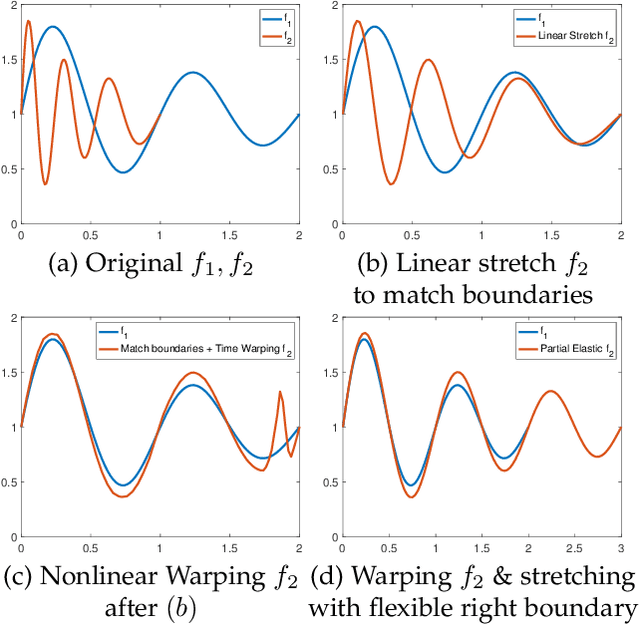
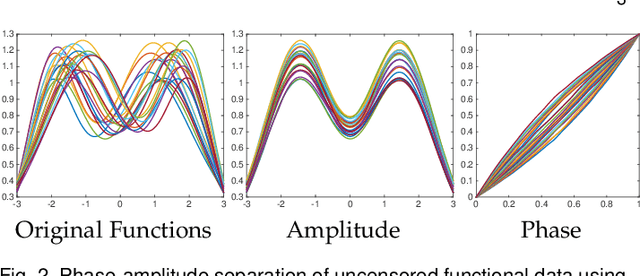

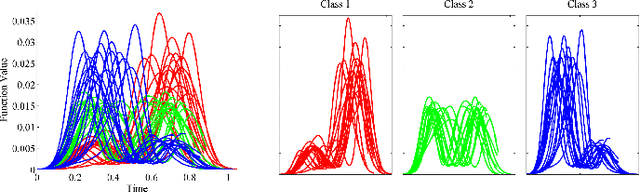
Abstract:Elastic Riemannian metrics have been used successfully in the past for statistical treatments of functional and curve shape data. However, this usage has suffered from an important restriction: the function boundaries are assumed fixed and matched. Functional data exhibiting unmatched boundaries typically arise from dynamical systems with variable evolution rates such as COVID-19 infection rate curves associated with different geographical regions. In this case, it is more natural to model such data with sliding boundaries and use partial matching, i.e., only a part of a function is matched to another function. Here, we develop a comprehensive Riemannian framework that allows for partial matching, comparing, and clustering of functions under both phase variability and uncertain boundaries. We extend past work by: (1) Forming a joint action of the time-warping and time-scaling groups; (2) Introducing a metric that is invariant to this joint action, allowing for a gradient-based approach to elastic partial matching; and (3) Presenting a modification that, while losing the metric property, allows one to control relative influence of the two groups. This framework is illustrated for registering and clustering shapes of COVID-19 rate curves, identifying essential patterns, minimizing mismatch errors, and reducing variability within clusters compared to previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge