Shape Analysis of Functional Data with Elastic Partial Matching
Paper and Code
May 18, 2021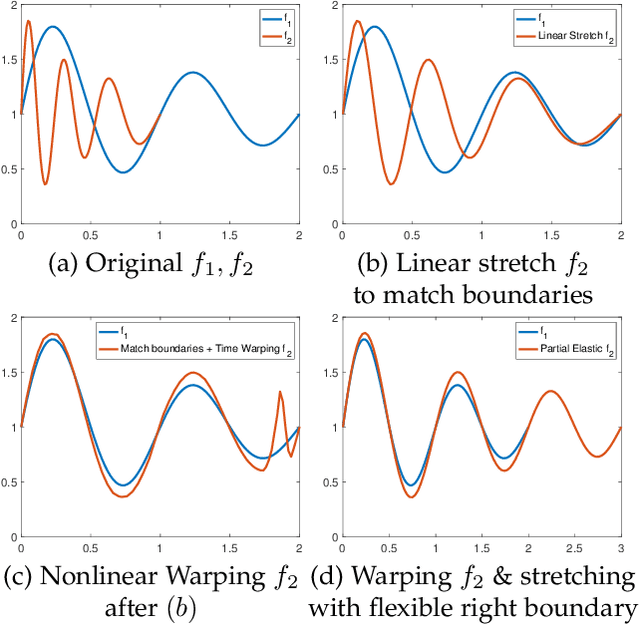
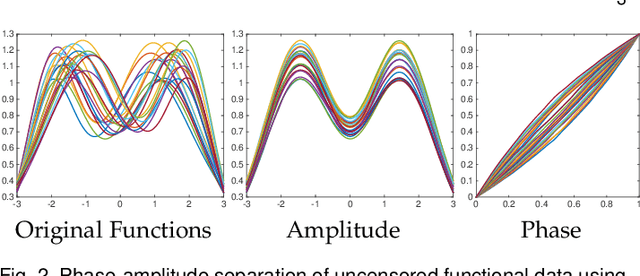

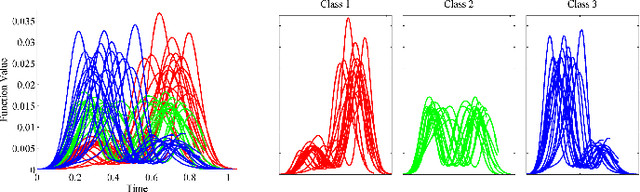
Elastic Riemannian metrics have been used successfully in the past for statistical treatments of functional and curve shape data. However, this usage has suffered from an important restriction: the function boundaries are assumed fixed and matched. Functional data exhibiting unmatched boundaries typically arise from dynamical systems with variable evolution rates such as COVID-19 infection rate curves associated with different geographical regions. In this case, it is more natural to model such data with sliding boundaries and use partial matching, i.e., only a part of a function is matched to another function. Here, we develop a comprehensive Riemannian framework that allows for partial matching, comparing, and clustering of functions under both phase variability and uncertain boundaries. We extend past work by: (1) Forming a joint action of the time-warping and time-scaling groups; (2) Introducing a metric that is invariant to this joint action, allowing for a gradient-based approach to elastic partial matching; and (3) Presenting a modification that, while losing the metric property, allows one to control relative influence of the two groups. This framework is illustrated for registering and clustering shapes of COVID-19 rate curves, identifying essential patterns, minimizing mismatch errors, and reducing variability within clusters compared to previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge