Topology-Driven Parallel Trajectory Optimization in Dynamic Environments

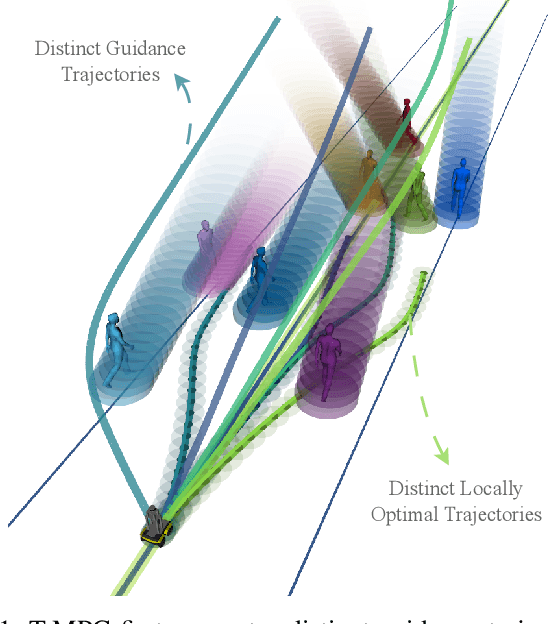
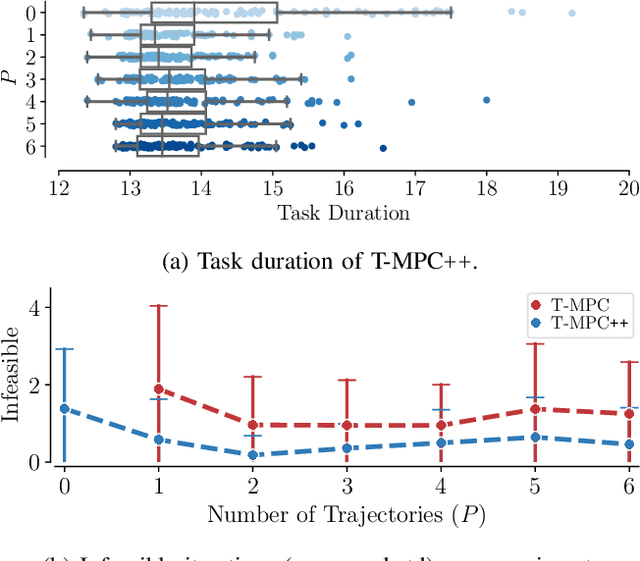
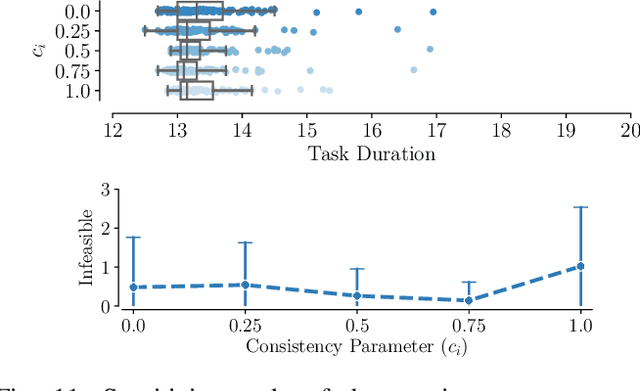
Ground robots navigating in complex, dynamic environments must compute collision-free trajectories to avoid obstacles safely and efficiently. Nonconvex optimization is a popular method to compute a trajectory in real-time. However, these methods often converge to locally optimal solutions and frequently switch between different local minima, leading to inefficient and unsafe robot motion. In this work, We propose a novel topology-driven trajectory optimization strategy for dynamic environments that plans multiple distinct evasive trajectories to enhance the robot's behavior and efficiency. A global planner iteratively generates trajectories in distinct homotopy classes. These trajectories are then optimized by local planners working in parallel. While each planner shares the same navigation objectives, they are locally constrained to a specific homotopy class, meaning each local planner attempts a different evasive maneuver. The robot then executes the feasible trajectory with the lowest cost in a receding horizon manner. We demonstrate, on a mobile robot navigating among pedestrians, that our approach leads to faster and safer trajectories than existing planners.

Scenario-Based Motion Planning with Bounded Probability of Collision

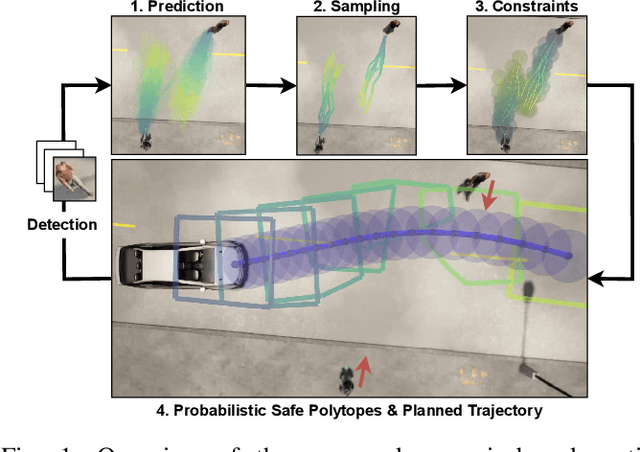
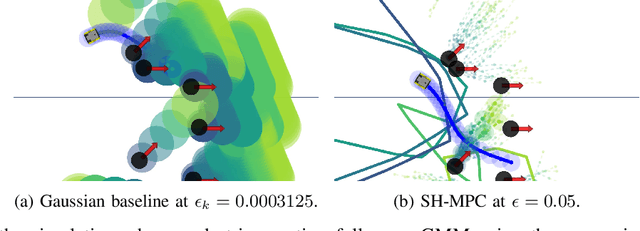
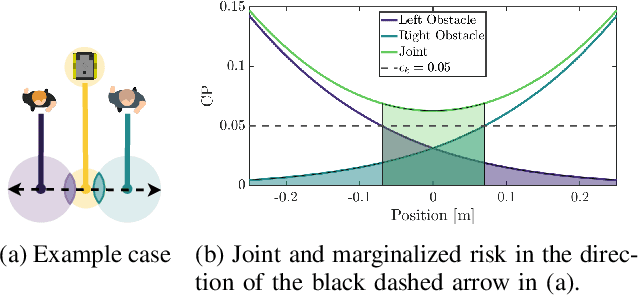
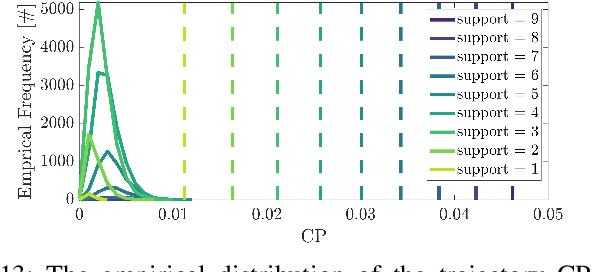
Robots will increasingly operate near humans that introduce uncertainties in the motion planning problem due to their complex nature. Typically, chance constraints are introduced in the planner to optimize performance while guaranteeing probabilistic safety. However, existing methods do not consider the actual probability of collision for the planned trajectory, but rather its marginalization, that is, the independent collision probabilities for each planning step and/or dynamic obstacle, resulting in conservative trajectories. To address this issue, we introduce a novel real-time capable method termed Safe Horizon MPC, that explicitly constrains the joint probability of collision with all obstacles over the duration of the motion plan. This is achieved by reformulating the chance-constrained planning problem using scenario optimization and predictive control. Our method is less conservative than state-of-the-art approaches, applicable to arbitrary probability distributions of the obstacles' trajectories, computationally tractable and scalable. We demonstrate our proposed approach using a mobile robot and an autonomous vehicle in an environment shared with humans.