Topology-Driven Parallel Trajectory Optimization in Dynamic Environments
Paper and Code
Jan 11, 2024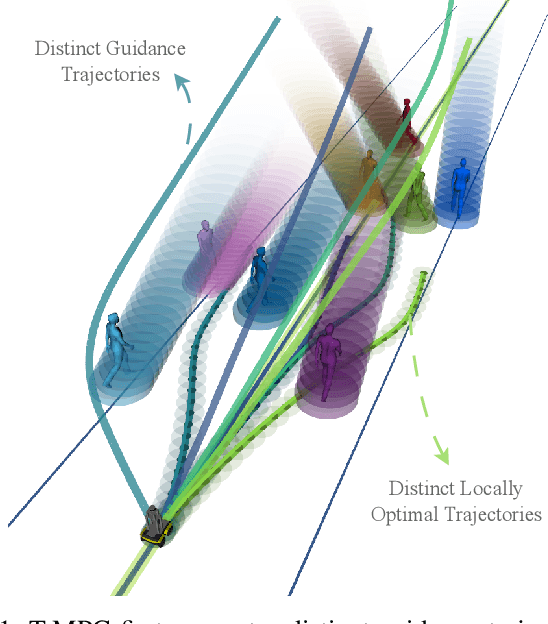
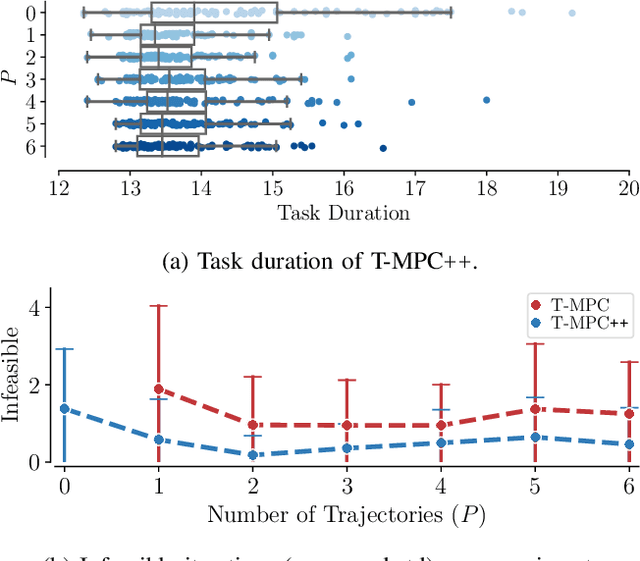
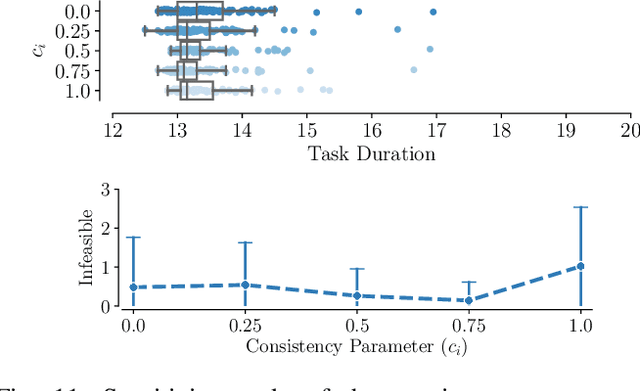

Ground robots navigating in complex, dynamic environments must compute collision-free trajectories to avoid obstacles safely and efficiently. Nonconvex optimization is a popular method to compute a trajectory in real-time. However, these methods often converge to locally optimal solutions and frequently switch between different local minima, leading to inefficient and unsafe robot motion. In this work, We propose a novel topology-driven trajectory optimization strategy for dynamic environments that plans multiple distinct evasive trajectories to enhance the robot's behavior and efficiency. A global planner iteratively generates trajectories in distinct homotopy classes. These trajectories are then optimized by local planners working in parallel. While each planner shares the same navigation objectives, they are locally constrained to a specific homotopy class, meaning each local planner attempts a different evasive maneuver. The robot then executes the feasible trajectory with the lowest cost in a receding horizon manner. We demonstrate, on a mobile robot navigating among pedestrians, that our approach leads to faster and safer trajectories than existing planners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge