An adaptive large neighborhood search heuristic for the multi-port continuous berth allocation problem

In this paper, we study a problem that integrates the vessel scheduling problem with the berth allocation into a collaborative problem denoted as the multi-port continuous berth allocation problem (MCBAP). This problem optimizes the berth allocation of a set of ships simultaneously in multiple ports while also considering the sailing speed of ships between ports. Due to the highly combinatorial character of the problem, exact methods struggle to scale to large-size instances, which points to exploring heuristic methods. We present a mixed-integer problem formulation for the MCBAP and introduce an adaptive large neighborhood search (ALNS) algorithm enhanced with a local search procedure to solve it. The computational results highlight the method's suitability for larger instances by providing high-quality solutions in short computational times. Practical insights indicate that the carriers' and terminal operators' operational costs are impacted in different ways by fuel prices, external ships at port, and the modeling of a continuous quay.

Generalized Multi-Output Gaussian Process Censored Regression

When modelling censored observations, a typical approach in current regression methods is to use a censored-Gaussian (i.e. Tobit) model to describe the conditional output distribution. In this paper, as in the case of missing data, we argue that exploiting correlations between multiple outputs can enable models to better address the bias introduced by censored data. To do so, we introduce a heteroscedastic multi-output Gaussian process model which combines the non-parametric flexibility of GPs with the ability to leverage information from correlated outputs under input-dependent noise conditions. To address the resulting inference intractability, we further devise a variational bound to the marginal log-likelihood suitable for stochastic optimization. We empirically evaluate our model against other generative models for censored data on both synthetic and real world tasks and further show how it can be generalized to deal with arbitrary likelihood functions. Results show how the added flexibility allows our model to better estimate the underlying non-censored (i.e. true) process under potentially complex censoring dynamics.

Estimating Latent Demand of Shared Mobility through Censored Gaussian Processes

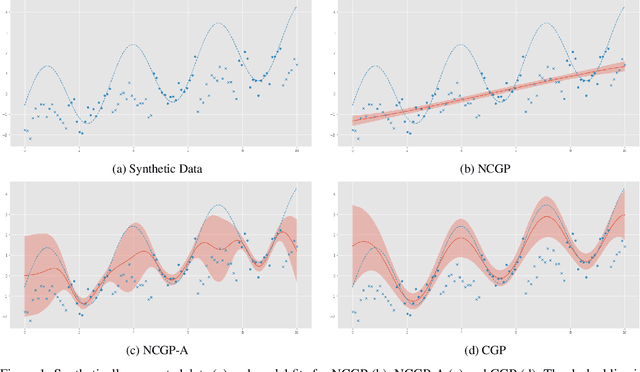
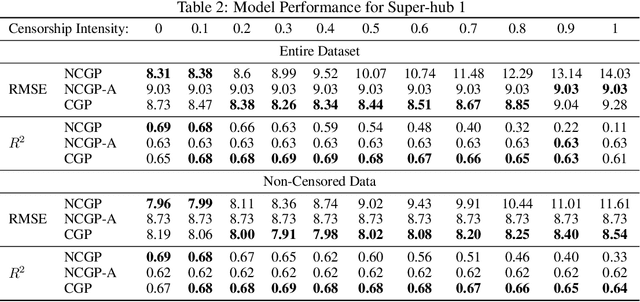
Transport demand is highly dependent on supply, especially for shared transport services where availability is often limited. As observed demand cannot be higher than available supply, historical transport data typically represents a biased, or censored, version of the true underlying demand pattern. Without explicitly accounting for this inherent distinction, predictive models of demand would necessarily represent a biased version of true demand, thus less effectively predicting the needs of service users. To counter this problem, we propose a general method for censorship-aware demand modeling, for which we devise a censored likelihood function. We apply this method to the task of shared mobility demand prediction by incorporating the censored likelihood within a Gaussian Process model, which can flexibly approximate arbitrary functional forms. Experiments on artificial and real-world datasets show how taking into account the limiting effect of supply on demand is essential in the process of obtaining an unbiased predictive model of user demand behavior.