Computational models of learning and synaptic plasticity

Many mathematical models of synaptic plasticity have been proposed to explain the diversity of plasticity phenomena observed in biological organisms. These models range from simple interpretations of Hebb's postulate, which suggests that correlated neural activity leads to increases in synaptic strength, to more complex rules that allow bidirectional synaptic updates, ensure stability, or incorporate additional signals like reward or error. At the same time, a range of learning paradigms can be observed behaviorally, from Pavlovian conditioning to motor learning and memory recall. Although it is difficult to directly link synaptic updates to learning outcomes experimentally, computational models provide a valuable tool for building evidence of this connection. In this chapter, we discuss several fundamental learning paradigms, along with the synaptic plasticity rules that might be used to implement them.

Biological learning in key-value memory networks

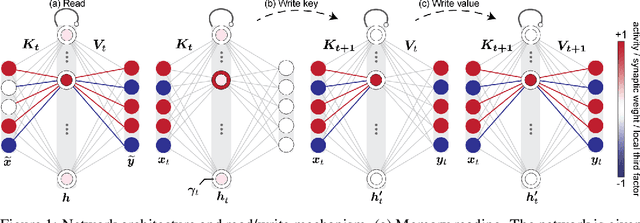
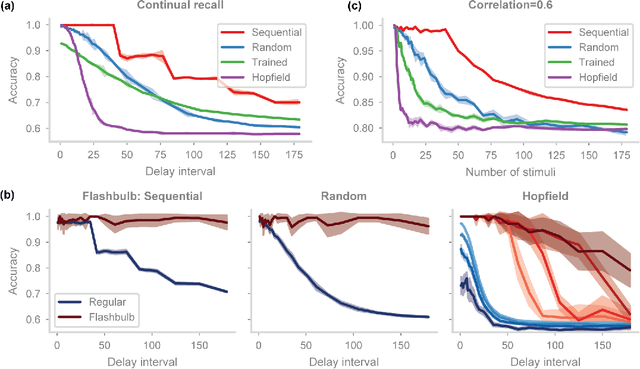
In neuroscience, classical Hopfield networks are the standard biologically plausible model of long-term memory, relying on Hebbian plasticity for storage and attractor dynamics for recall. In contrast, memory-augmented neural networks in machine learning commonly use a key-value mechanism to store and read out memories in a single step. Such augmented networks achieve impressive feats of memory compared to traditional variants, yet their biological relevance is unclear. We propose an implementation of basic key-value memory that stores inputs using a combination of biologically plausible three-factor plasticity rules. The same rules are recovered when network parameters are meta-learned. Our network performs on par with classical Hopfield networks on autoassociative memory tasks and can be naturally extended to continual recall, heteroassociative memory, and sequence learning. Our results suggest a compelling alternative to the classical Hopfield network as a model of biological long-term memory.