Gradient-only line searches: An Alternative to Probabilistic Line Searches

Step sizes in neural network training are largely determined using predetermined rules such as fixed learning rates and learning rate schedules, which require user input to determine their functional form and associated hyperparameters. Global optimization strategies to resolve these hyperparameters are computationally expensive. Line searches are capable of adaptively resolving learning rate schedules. However, due to discontinuities induced by mini-batch sampling, they have largely fallen out of favor. Notwithstanding, probabilistic line searches have recently demonstrated viability in resolving learning rates for stochastic loss functions. This method creates surrogates with confidence intervals, where restrictions are placed on the rate at which the search domain can grow along a search direction. This paper introduces an alternative paradigm, Gradient-Only Line Searches that are inexact (GOLS-I), as an alternative strategy to automatically resolve learning rates in stochastic cost functions over a range of 15 orders of magnitude without the use of surrogates. We show that GOLS-I is a competitive strategy to reliably resolve step sizes, adding high value in terms of performance, while being easy to implement. Considering mini-batch sampling, we open the discussion on how to split the effort to resolve quality search directions from quality step size estimates along a search direction.

Visual interpretation of the robustness of Non-Negative Associative Gradient Projection Points over function minimizers in mini-batch sampled loss functions

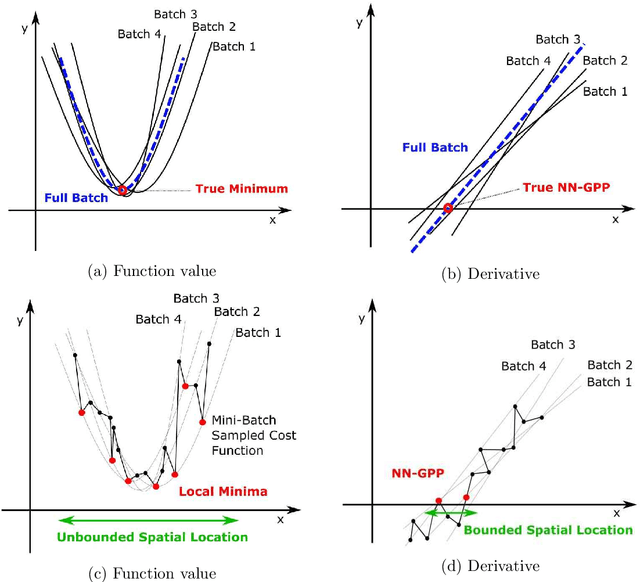
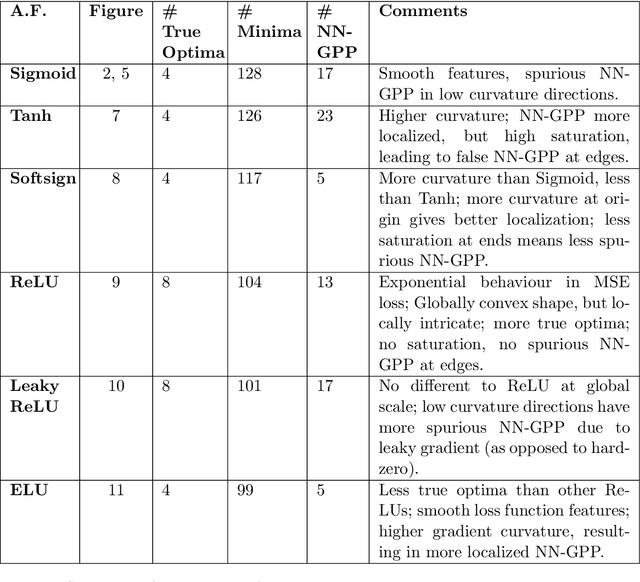
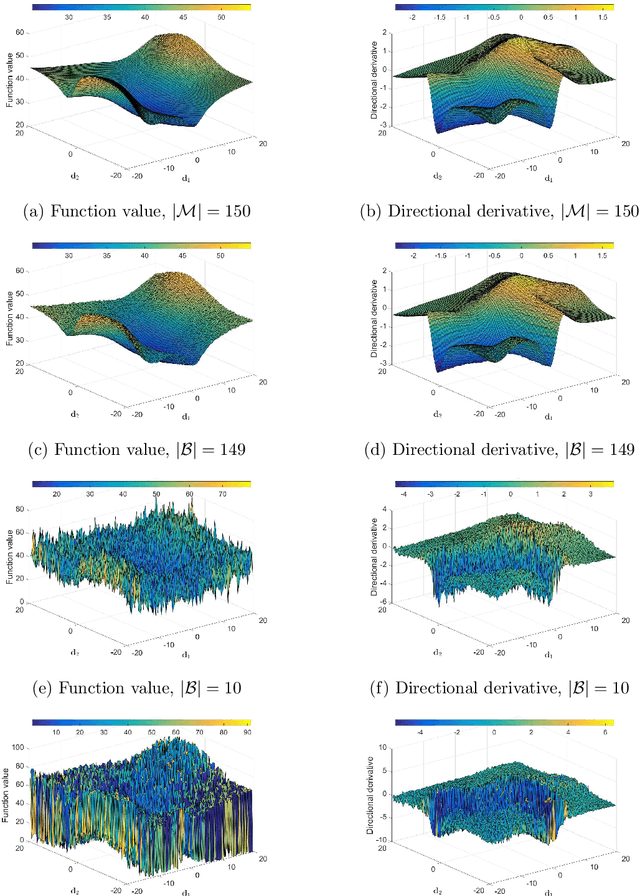
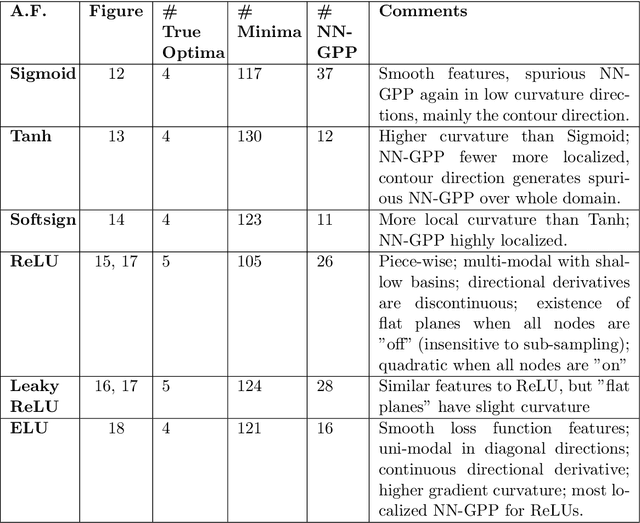
Mini-batch sub-sampling is likely here to stay, due to growing data demands, memory-limited computational resources such as graphical processing units (GPUs), and the dynamics of on-line learning. Sampling a new mini-batch at every loss evaluation brings a number of benefits, but also one significant drawback: The loss function becomes discontinuous. These discontinuities are generally not problematic when using fixed learning rates or learning rate schedules typical of subgradient methods. However, they hinder attempts to directly minimize the loss function by solving for critical points, since function minimizers find spurious minima induced by discontinuities, while critical points may not even exist. Therefore, finding function minimizers and critical points in stochastic optimization is ineffective. As a result, attention has been given to reducing the effect of these discontinuities by means such as gradient averaging or adaptive and dynamic sampling. This paper offers an alternative paradigm: Recasting the optimization problem to rather find Non-Negative Associated Gradient Projection Points (NN-GPPs). In this paper, we demonstrate the NN-GPP interpretation of gradient information is more robust than critical points or minimizers, being less susceptible to sub-sampling induced variance and eliminating spurious function minimizers. We conduct a visual investigation, where we compare function value and gradient information for a variety of popular activation functions as applied to a simple neural network training problem. Based on the improved description offered by NN-GPPs over minimizers to identify true optima, in particular when using smooth activation functions with high curvature characteristics, we postulate that locating NN-GPPs can contribute significantly to automating neural network training.