Daniel Tschernutter
A Globally Convergent Algorithm for Neural Network Parameter Optimization Based on Difference-of-Convex Functions
Jan 15, 2024Abstract:We propose an algorithm for optimizing the parameters of single hidden layer neural networks. Specifically, we derive a blockwise difference-of-convex (DC) functions representation of the objective function. Based on the latter, we propose a block coordinate descent (BCD) approach that we combine with a tailored difference-of-convex functions algorithm (DCA). We prove global convergence of the proposed algorithm. Furthermore, we mathematically analyze the convergence rate of parameters and the convergence rate in value (i.e., the training loss). We give conditions under which our algorithm converges linearly or even faster depending on the local shape of the loss function. We confirm our theoretical derivations numerically and compare our algorithm against state-of-the-art gradient-based solvers in terms of both training loss and test loss.
Interpretable Off-Policy Learning via Hyperbox Search
Mar 04, 2022



Abstract:Personalized treatment decisions have become an integral part of modern medicine. Thereby, the aim is to make treatment decisions based on individual patient characteristics. Numerous methods have been developed for learning such policies from observational data that achieve the best outcome across a certain policy class. Yet these methods are rarely interpretable. However, interpretability is often a prerequisite for policy learning in clinical practice. In this paper, we propose an algorithm for interpretable off-policy learning via hyperbox search. In particular, our policies can be represented in disjunctive normal form (i.e., OR-of-ANDs) and are thus intelligible. We prove a universal approximation theorem that shows that our policy class is flexible enough to approximate any measurable function arbitrarily well. For optimization, we develop a tailored column generation procedure within a branch-and-bound framework. Using a simulation study, we demonstrate that our algorithm outperforms state-of-the-art methods from interpretable off-policy learning in terms of regret. Using real-word clinical data, we perform a user study with actual clinical experts, who rate our policies as highly interpretable.
Generalizing Off-Policy Learning under Sample Selection Bias
Dec 02, 2021
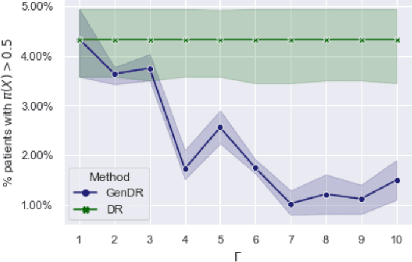

Abstract:Learning personalized decision policies that generalize to the target population is of great relevance. Since training data is often not representative of the target population, standard policy learning methods may yield policies that do not generalize target population. To address this challenge, we propose a novel framework for learning policies that generalize to the target population. For this, we characterize the difference between the training data and the target population as a sample selection bias using a selection variable. Over an uncertainty set around this selection variable, we optimize the minimax value of a policy to achieve the best worst-case policy value on the target population. In order to solve the minimax problem, we derive an efficient algorithm based on a convex-concave procedure and prove convergence for parametrized spaces of policies such as logistic policies. We prove that, if the uncertainty set is well-specified, our policies generalize to the target population as they can not do worse than on the training data. Using simulated data and a clinical trial, we demonstrate that, compared to standard policy learning methods, our framework improves the generalizability of policies substantially.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge