Edge2Vec: A High Quality Embedding for the Jigsaw Puzzle Problem

Pairwise compatibility measure (CM) is a key component in solving the jigsaw puzzle problem (JPP) and many of its recently proposed variants. With the rapid rise of deep neural networks (DNNs), a trade-off between performance (i.e., accuracy) and computational efficiency has become a very significant issue. Whereas an end-to-end DNN-based CM model exhibits high performance, it becomes virtually infeasible on very large puzzles, due to its highly intensive computation. On the other hand, exploiting the concept of embeddings to alleviate significantly the computational efficiency, has resulted in degraded performance, according to recent studies. This paper derives an advanced CM model (based on modified embeddings and a new loss function, called hard batch triplet loss) for closing the above gap between speed and accuracy; namely a CM model that achieves SOTA results in terms of performance and efficiency combined. We evaluated our newly derived CM on three commonly used datasets, and obtained a reconstruction improvement of 5.8% and 19.5% for so-called Type-1 and Type-2 problem variants, respectively, compared to best known results due to previous CMs.

TEN: Twin Embedding Networks for the Jigsaw Puzzle Problem with Eroded Boundaries

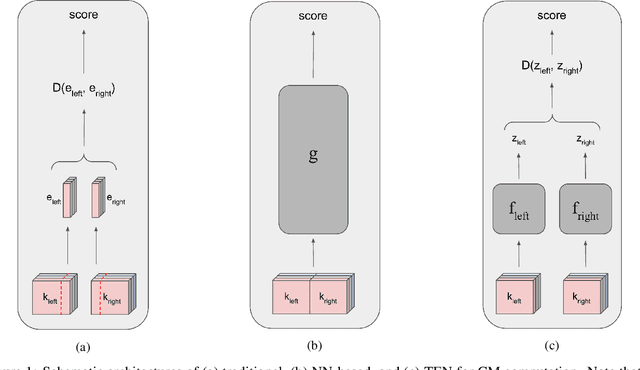
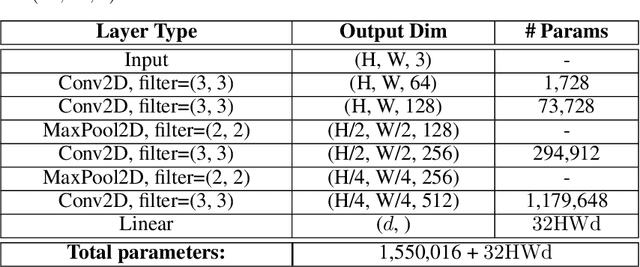
The jigsaw puzzle problem (JPP) is a well-known research problem, which has been studied for many years. Solving this problem typically involves a two-stage scheme, consisting of the computation of a pairwise piece compatibility measure (CM), coupled with a subsequent puzzle reconstruction algorithm. Many effective CMs, which apply a simple distance measure, based merely on the information along the piece edges, have been proposed. However, the practicality of these classical methods is rather doubtful for problem instances harder than pure synthetic images. Specifically, these methods tend to break down in more realistic scenarios involving, e.g., monochromatic puzzles, eroded boundaries due to piece degradation over long time periods, missing pieces, etc. To overcome this significant deficiency, a few deep convolutional neural network (CNN)-based CMs have been recently introduced. Despite their promising accuracy, these models are very computationally intensive. Twin Embedding Networks (TEN), to represent a piece with respect to its boundary in a latent embedding space. Combining this latent representation with a simple distance measure, we then demonstrate a superior performance, in terms of accuracy, of our newly proposed pairwise CM, compared to that of various classical methods, for the problem domain of eroded tile boundaries, a testbed for a number of real-world JPP variants. Furthermore, we also demonstrate that TEN is faster by a few orders of magnitude, on average, than the recent NN models, i.e., it is as fast as the classical methods. In this regard, the paper makes a significant first attempt at bridging the gap between the relatively low accuracy (of classical methods) and the intensive computational complexity (of NN models), for practical, real-world puzzle-like problems.

A Novel Hybrid Scheme Using Genetic Algorithms and Deep Learning for the Reconstruction of Portuguese Tile Panels

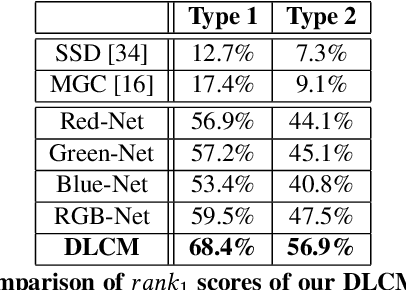
This paper presents a novel scheme, based on a unique combination of genetic algorithms (GAs) and deep learning (DL), for the automatic reconstruction of Portuguese tile panels, a challenging real-world variant of the jigsaw puzzle problem (JPP) with important national heritage implications. Specifically, we introduce an enhanced GA-based puzzle solver, whose integration with a novel DL-based compatibility measure (DLCM) yields state-of-the-art performance, regarding the above application. Current compatibility measures consider typically (the chromatic information of) edge pixels (between adjacent tiles), and help achieve high accuracy for the synthetic JPP variant. However, such measures exhibit rather poor performance when applied to the Portuguese tile panels, which are susceptible to various real-world effects, e.g., monochromatic panels, non-squared tiles, edge degradation, etc. To overcome such difficulties, we have developed a novel DLCM to extract high-level texture/color statistics from the entire tile information. Integrating this measure with our enhanced GA-based puzzle solver, we have demonstrated, for the first time, how to deal most effectively with large-scale real-world problems, such as the Portuguese tile problem. Specifically, we have achieved 82% accuracy for the reconstruction of Portuguese tile panels with unknown piece rotation and puzzle dimension (compared to merely 3.5% average accuracy achieved by the best method known for solving this problem variant). The proposed method outperforms even human experts in several cases, correcting their mistakes in the manual tile assembly.