TEN: Twin Embedding Networks for the Jigsaw Puzzle Problem with Eroded Boundaries

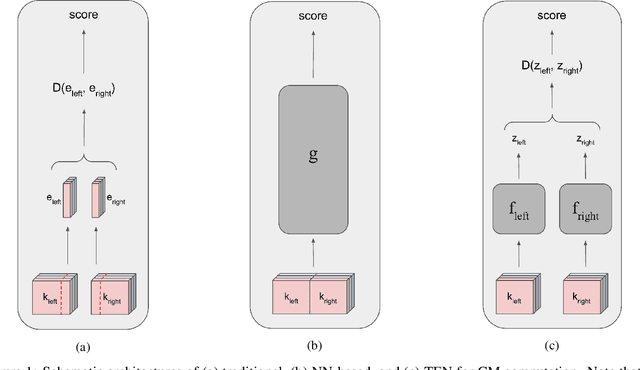
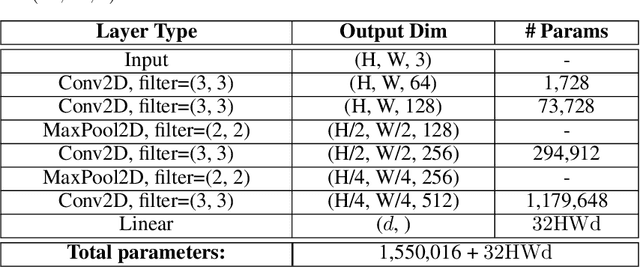
The jigsaw puzzle problem (JPP) is a well-known research problem, which has been studied for many years. Solving this problem typically involves a two-stage scheme, consisting of the computation of a pairwise piece compatibility measure (CM), coupled with a subsequent puzzle reconstruction algorithm. Many effective CMs, which apply a simple distance measure, based merely on the information along the piece edges, have been proposed. However, the practicality of these classical methods is rather doubtful for problem instances harder than pure synthetic images. Specifically, these methods tend to break down in more realistic scenarios involving, e.g., monochromatic puzzles, eroded boundaries due to piece degradation over long time periods, missing pieces, etc. To overcome this significant deficiency, a few deep convolutional neural network (CNN)-based CMs have been recently introduced. Despite their promising accuracy, these models are very computationally intensive. Twin Embedding Networks (TEN), to represent a piece with respect to its boundary in a latent embedding space. Combining this latent representation with a simple distance measure, we then demonstrate a superior performance, in terms of accuracy, of our newly proposed pairwise CM, compared to that of various classical methods, for the problem domain of eroded tile boundaries, a testbed for a number of real-world JPP variants. Furthermore, we also demonstrate that TEN is faster by a few orders of magnitude, on average, than the recent NN models, i.e., it is as fast as the classical methods. In this regard, the paper makes a significant first attempt at bridging the gap between the relatively low accuracy (of classical methods) and the intensive computational complexity (of NN models), for practical, real-world puzzle-like problems.