A Note on Rough Set Algebra and Core Regular Double Stone Algebras

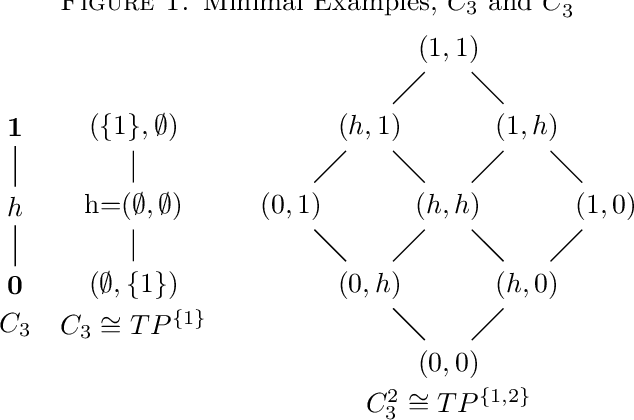
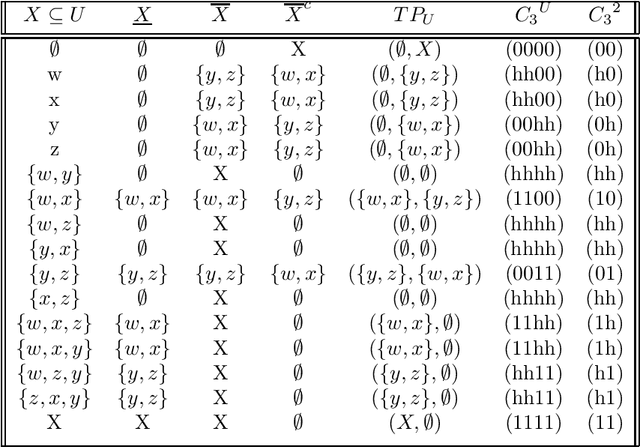
Given an approximation space $\langle U,\theta \rangle$, assume that $E$ is the indexing set for the equivalence classes of $\theta$ and let $R_\theta$ denote the collection of rough sets of the form $\langle\underline{X},\overline{X}\rangle$ as a regular double Stone algebra and what I. Dunstch referred to as a Katrinak algebra.[7],[8] We give an alternate proof from the one given in [1] of the fact that if $|\theta_u| > 1\ \forall\ u \in U$ then $R_\theta$ is a core regular double Stone algebra. Further let $C_3$ denote the 3 element chain as a core regular double Stone algebra and $TP_U$ denote the collection of ternary partitions over the set $U$. In our Main Theorem we show $R_\theta$ with $|\theta_u| > 1\ \forall\ u \in U$ to be isomorphic to $TP_E$ and $C_3^E$, with $E$ is an indexing set for $\theta$, and that the three CRDSA's are complete and atomic. We feel this could be very useful when dealing with a specific $R_\theta$ in an application. In our Main Corollary we show explicitly how we can embed such $R_\theta$ in $TP_U$, $C_3^U$, respectively, $\phi\circ \alpha_r:R_\theta\hookrightarrow TP_U\hookrightarrow C_3^U$, and hence identify it with its specific images. Following in the footsteps of Theorem 3. and Corollary 2.4 of [7], we show $C_3^J \cong R_\theta$ for $\langle U,\theta \rangle$ the approximation space given by $U = J \times \{0,1\}$, $\theta = \{(j0),(j1)\} : j \in J\}$ and every CRDSA is isomorphic to a subalgebra of a principal rough set algebra, $R_\theta$, for some approximation space $\langle U,\theta \rangle$. Finally, we demonstrate this and our Main Theorem by expanding an example from [1]. Further, we know a little more about the subalgebras of $TP_U$ and $C_3^U$ in general as they must exist for every $E$ that is an indexing set for the equivalence classes of any equivalence relation $\theta$ on $U$ satisfying $|\theta_u| > 1\ \forall\ u \in U$.

Advancing the Research and Development of Assured Artificial Intelligence and Machine Learning Capabilities

Artificial intelligence (AI) and machine learning (ML) have become increasingly vital in the development of novel defense and intelligence capabilities across all domains of warfare. An adversarial AI (A2I) and adversarial ML (AML) attack seeks to deceive and manipulate AI/ML models. It is imperative that AI/ML models can defend against these attacks. A2I/AML defenses will help provide the necessary assurance of these advanced capabilities that use AI/ML models. The A2I Working Group (A2IWG) seeks to advance the research and development of assured AI/ML capabilities via new A2I/AML defenses by fostering a collaborative environment across the U.S. Department of Defense and U.S. Intelligence Community. The A2IWG aims to identify specific challenges that it can help solve or address more directly, with initial focus on three topics: AI Trusted Robustness, AI System Security, and AI/ML Architecture Vulnerabilities.