A Note on Rough Set Algebra and Core Regular Double Stone Algebras

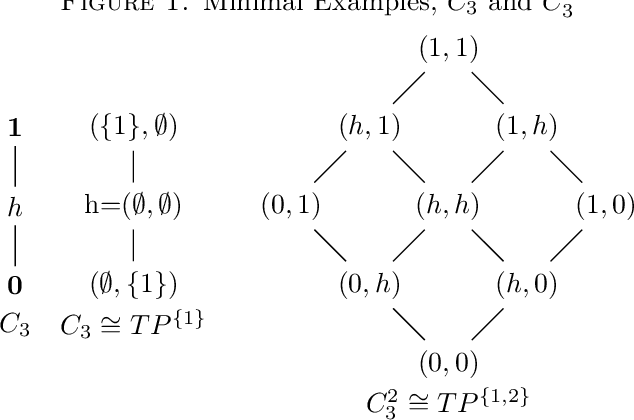
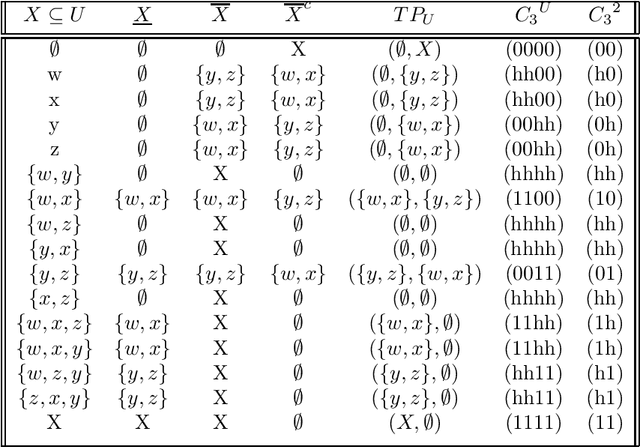
Given an approximation space $\langle U,\theta \rangle$, assume that $E$ is the indexing set for the equivalence classes of $\theta$ and let $R_\theta$ denote the collection of rough sets of the form $\langle\underline{X},\overline{X}\rangle$ as a regular double Stone algebra and what I. Dunstch referred to as a Katrinak algebra.[7],[8] We give an alternate proof from the one given in [1] of the fact that if $|\theta_u| > 1\ \forall\ u \in U$ then $R_\theta$ is a core regular double Stone algebra. Further let $C_3$ denote the 3 element chain as a core regular double Stone algebra and $TP_U$ denote the collection of ternary partitions over the set $U$. In our Main Theorem we show $R_\theta$ with $|\theta_u| > 1\ \forall\ u \in U$ to be isomorphic to $TP_E$ and $C_3^E$, with $E$ is an indexing set for $\theta$, and that the three CRDSA's are complete and atomic. We feel this could be very useful when dealing with a specific $R_\theta$ in an application. In our Main Corollary we show explicitly how we can embed such $R_\theta$ in $TP_U$, $C_3^U$, respectively, $\phi\circ \alpha_r:R_\theta\hookrightarrow TP_U\hookrightarrow C_3^U$, and hence identify it with its specific images. Following in the footsteps of Theorem 3. and Corollary 2.4 of [7], we show $C_3^J \cong R_\theta$ for $\langle U,\theta \rangle$ the approximation space given by $U = J \times \{0,1\}$, $\theta = \{(j0),(j1)\} : j \in J\}$ and every CRDSA is isomorphic to a subalgebra of a principal rough set algebra, $R_\theta$, for some approximation space $\langle U,\theta \rangle$. Finally, we demonstrate this and our Main Theorem by expanding an example from [1]. Further, we know a little more about the subalgebras of $TP_U$ and $C_3^U$ in general as they must exist for every $E$ that is an indexing set for the equivalence classes of any equivalence relation $\theta$ on $U$ satisfying $|\theta_u| > 1\ \forall\ u \in U$.