Uncertainty-Aware Dual-Ranking Strategy for Offline Data-Driven Multi-Objective Optimization

Offline data-driven Multi-Objective Optimization Problems (MOPs) rely on limited data from simulations, experiments, or sensors. This scarcity leads to high epistemic uncertainty in surrogate predictions. Conventional surrogate methods such as Kriging assume Gaussian distributions, which can yield suboptimal results when the assumptions fail. To address these issues, we propose a simple yet novel dual-ranking strategy, working with a basic multi-objective evolutionary algorithm, NSGA-II, where the built-in non-dominated sorting is kept and the second rank is devised for uncertainty estimation. In the latter, we utilize the uncertainty estimates given by several surrogate models, including Quantile Regression (QR), Monte Carlo Dropout (MCD), and Bayesian Neural Networks (BNNs). Concretely, with this dual-ranking strategy, each solution's final rank is the average of its non-dominated sorting rank and a rank derived from the uncertainty-adjusted fitness function, thus reducing the risk of misguided optimization under data constraints. We evaluate our approach on benchmark and real-world MOPs, comparing it to state-of-the-art methods. The results show that our dual-ranking strategy significantly improves the performance of NSGA-II in offline settings, achieving competitive outcomes compared with traditional surrogate-based methods. This framework advances uncertainty-aware multi-objective evolutionary algorithms, offering a robust solution for data-limited, real-world applications.

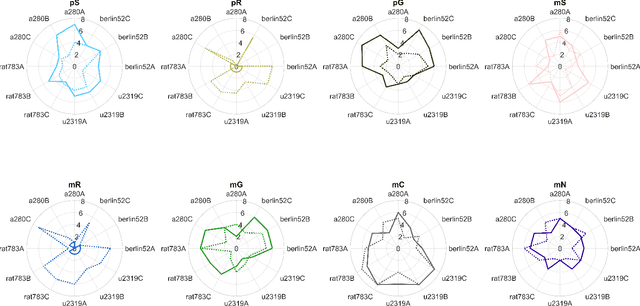
iTARGET: Interpretable Tailored Age Regression for Grouped Epigenetic Traits

Accurately predicting chronological age from DNA methylation patterns is crucial for advancing biological age estimation. However, this task is made challenging by Epigenetic Correlation Drift (ECD) and Heterogeneity Among CpGs (HAC), which reflect the dynamic relationship between methylation and age across different life stages. To address these issues, we propose a novel two-phase algorithm. The first phase employs similarity searching to cluster methylation profiles by age group, while the second phase uses Explainable Boosting Machines (EBM) for precise, group-specific prediction. Our method not only improves prediction accuracy but also reveals key age-related CpG sites, detects age-specific changes in aging rates, and identifies pairwise interactions between CpG sites. Experimental results show that our approach outperforms traditional epigenetic clocks and machine learning models, offering a more accurate and interpretable solution for biological age estimation with significant implications for aging research.

Reproducibility and Baseline Reporting for Dynamic Multi-objective Benchmark Problems

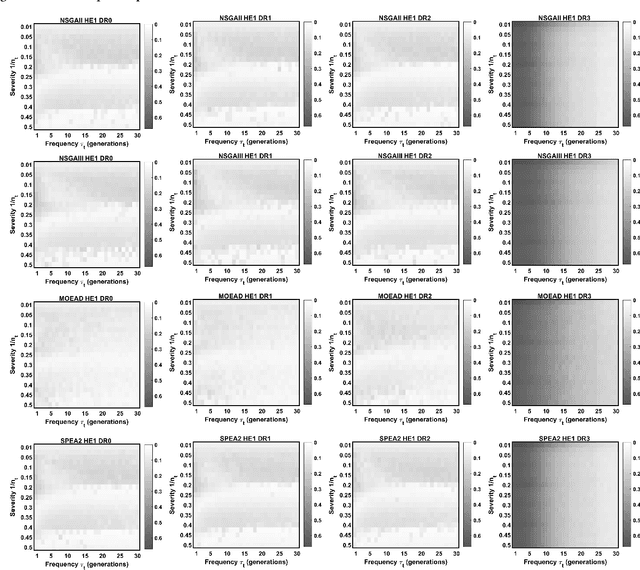
Dynamic multi-objective optimization problems (DMOPs) are widely accepted to be more challenging than stationary problems due to the time-dependent nature of the objective functions and/or constraints. Evaluation of purpose-built algorithms for DMOPs is often performed on narrow selections of dynamic instances with differing change magnitude and frequency or a limited selection of problems. In this paper, we focus on the reproducibility of simulation experiments for parameters of DMOPs. Our framework is based on an extension of PlatEMO, allowing for the reproduction of results and performance measurements across a range of dynamic settings and problems. A baseline schema for dynamic algorithm evaluation is introduced, which provides a mechanism to interrogate performance and optimization behaviours of well-known evolutionary algorithms that were not designed specifically for DMOPs. Importantly, by determining the maximum capability of non-dynamic multi-objective evolutionary algorithms, we can establish the minimum capability required of purpose-built dynamic algorithms to be useful. The simplest modifications to manage dynamic changes introduce diversity. Allowing non-dynamic algorithms to incorporate mutated/random solutions after change events determines the improvement possible with minor algorithm modifications. Future expansion to include current dynamic algorithms will enable reproduction of their results and verification of their abilities and performance across DMOP benchmark space.

Dynamic Multi-objective Optimization of the Travelling Thief Problem

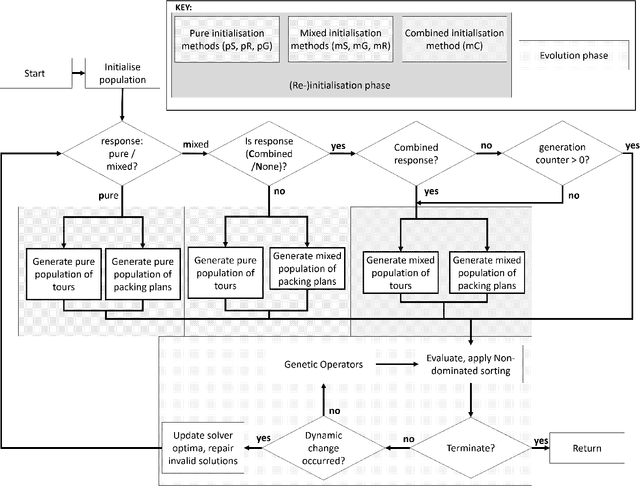
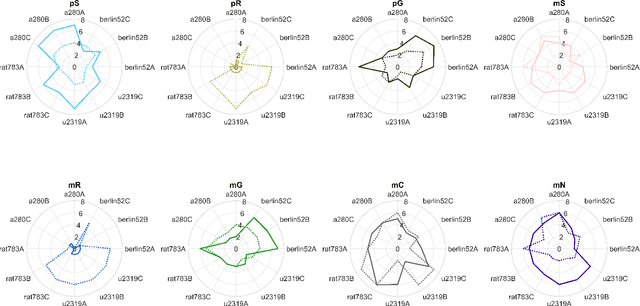
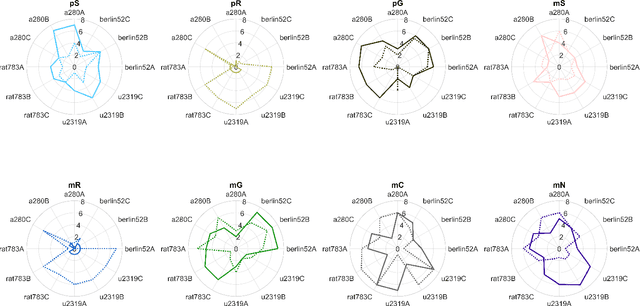
Investigation of detailed and complex optimisation problem formulations that reflect realistic scenarios is a burgeoning field of research. A growing body of work exists for the Travelling Thief Problem, including multi-objective formulations and comparisons of exact and approximate methods to solve it. However, as many realistic scenarios are non-static in time, dynamic formulations have yet to be considered for the TTP. Definition of dynamics within three areas of the TTP problem are addressed; in the city locations, availability map and item values. Based on the elucidation of solution conservation between initial sets and obtained non-dominated sets, we define a range of initialisation mechanisms using solutions generated via solvers, greedily and randomly. These are then deployed to seed the population after a change and the performance in terms of hypervolume and spread is presented for comparison. Across a range of problems with varying TSP-component and KP-component sizes, we observe interesting trends in line with existing conclusions; there is little benefit to using randomisation as a strategy for initialisation of solution populations when the optimal TSP and KP component solutions can be exploited. Whilst these separate optima don't guarantee good TTP solutions, when combined, provide better initial performance and therefore in some examined instances, provides the best response to dynamic changes. A combined approach that mixes solution generation methods to provide a composite population in response to dynamic changes provides improved performance in some instances for the different dynamic TTP formulations. Potential for further development of a more cooperative combined method are realised to more cohesively exploit known information about the problems.