Semi-Supervised Clustering with Inaccurate Pairwise Annotations

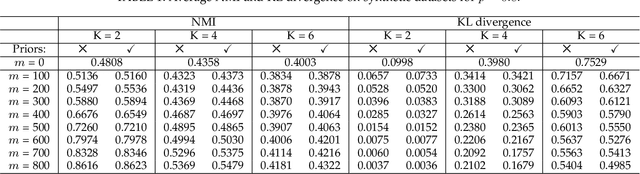
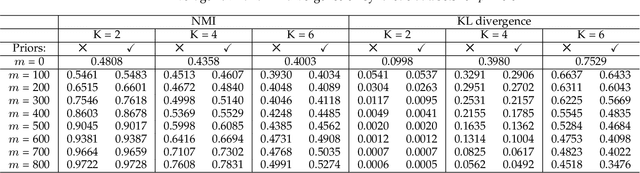
Pairwise relational information is a useful way of providing partial supervision in domains where class labels are difficult to acquire. This work presents a clustering model that incorporates pairwise annotations in the form of must-link and cannot-link relations and considers possible annotation inaccuracies (i.e., a common setting when experts provide pairwise supervision). We propose a generative model that assumes Gaussian-distributed data samples along with must-link and cannot-link relations generated by stochastic block models. We adopt a maximum-likelihood approach and demonstrate that, even when supervision is weak and inaccurate, accounting for relational information significantly improves clustering performance. Relational information also helps to detect meaningful groups in real-world datasets that do not fit the original data-distribution assumptions. Additionally, we extend the model to integrate prior knowledge of experts' accuracy and discuss circumstances in which the use of this knowledge is beneficial.

Assortative-Constrained Stochastic Block Models

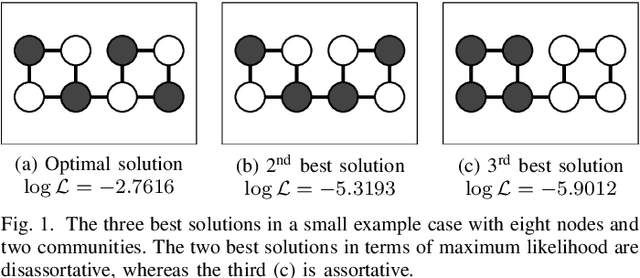
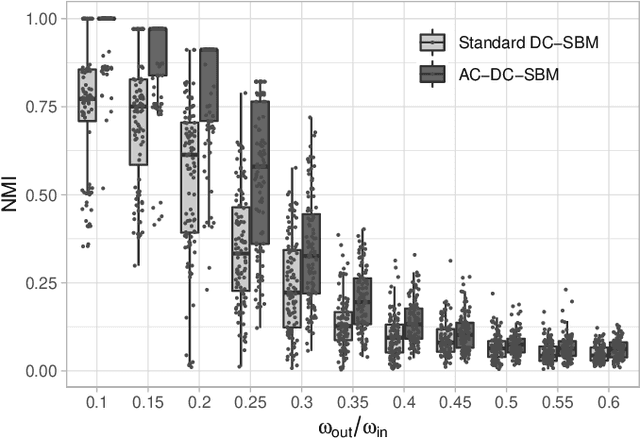
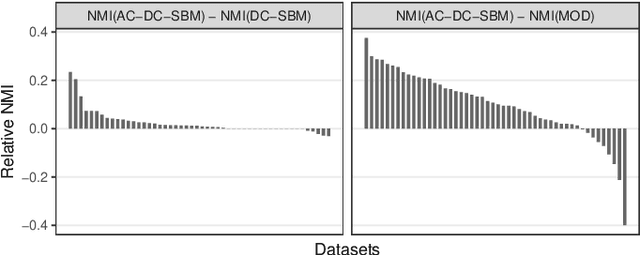
Stochastic block models (SBMs) are often used to find assortative community structures in networks, such that the probability of connections within communities is higher than in between communities. However, classic SBMs are not limited to assortative structures. In this study, we discuss the implications of this model-inherent indifference towards assortativity or disassortativity, and show that this characteristic can lead to undesirable outcomes for networks which are presupposedy assortative but which contain a reduced amount of information. To circumvent this issue, we introduce a constrained SBM that imposes strong assortativity constraints, along with efficient algorithmic approaches to solve it. These constraints significantly boost community recovery capabilities in regimes that are close to the information-theoretic threshold. They also permit to identify structurally-different communities in networks representing cerebral-cortex activity regions.

HG-means: A scalable hybrid genetic algorithm for minimum sum-of-squares clustering

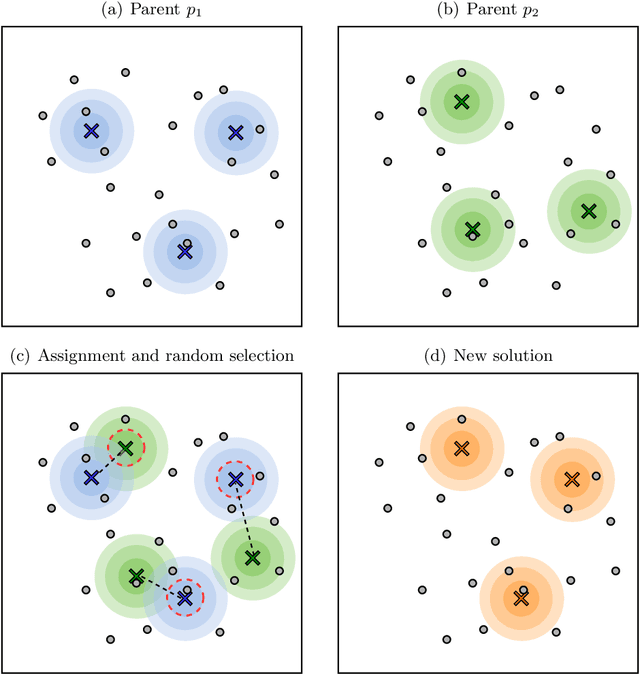
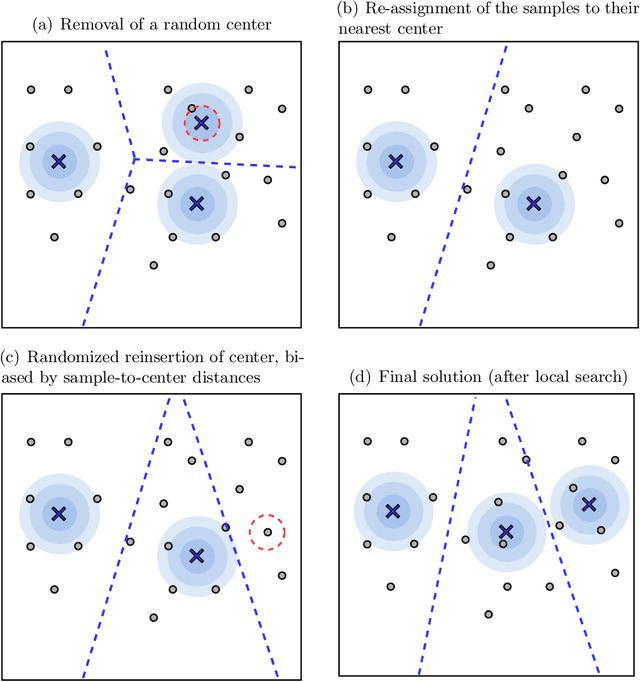
Minimum sum-of-squares clustering (MSSC) is a widely used clustering model, of which the popular K-means algorithm constitutes a local minimizer. It is well known that the solutions of K-means can be arbitrarily distant from the true MSSC global optimum, and dozens of alternative heuristics have been proposed for this problem. However, no other algorithm has been commonly adopted in the literature. This may be related to differences of computational effort, or to the assumption that a better solution of the MSSC has only a minor impact on classification or generalization capabilities. In this article, we dispute this belief. We introduce an efficient population-based metaheuristic that uses K-means as a local search in combination with problem-tailored crossover, mutation, and diversification operators. This algorithm can be interpreted as a multi-start K-means, in which the initial center positions are carefully sampled based on the search history. The approach is scalable and accurate, outperforming all recent state-of-the-art algorithms for MSSC in terms of solution quality, measured by the depth of local minima. This enhanced accuracy leads to classification results which are significantly closer to the ground truth than those of other algorithms, for overlapping Gaussian-mixture datasets with a large number of features and clusters. Therefore, improved global optimization methods appear to be essential to better exploit the MSSC model in high dimension.