A Correlation- and Mean-Aware Loss Function and Benchmarking Framework to Improve GAN-based Tabular Data Synthesis

Advancements in science rely on data sharing. In medicine, where personal data are often involved, synthetic tabular data generated by generative adversarial networks (GANs) offer a promising avenue. However, existing GANs struggle to capture the complexities of real-world tabular data, which often contain a mix of continuous and categorical variables with potential imbalances and dependencies. We propose a novel correlation- and mean-aware loss function designed to address these challenges as a regularizer for GANs. To ensure a rigorous evaluation, we establish a comprehensive benchmarking framework using ten real-world datasets and eight established tabular GAN baselines. The proposed loss function demonstrates statistically significant improvements over existing methods in capturing the true data distribution, significantly enhancing the quality of synthetic data generated with GANs. The benchmarking framework shows that the enhanced synthetic data quality leads to improved performance in downstream machine learning (ML) tasks, ultimately paving the way for easier data sharing.

Mapping higher-order network flows in memory and multilayer networks with Infomap

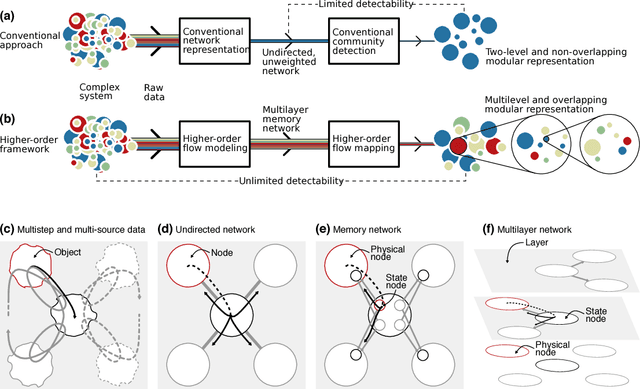
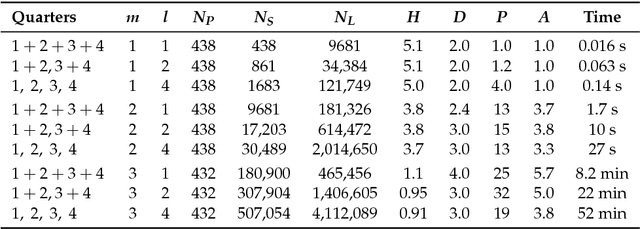
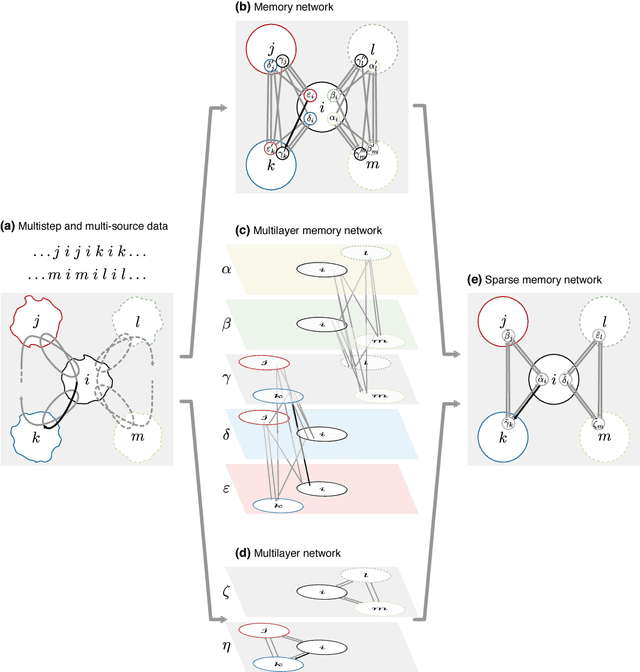
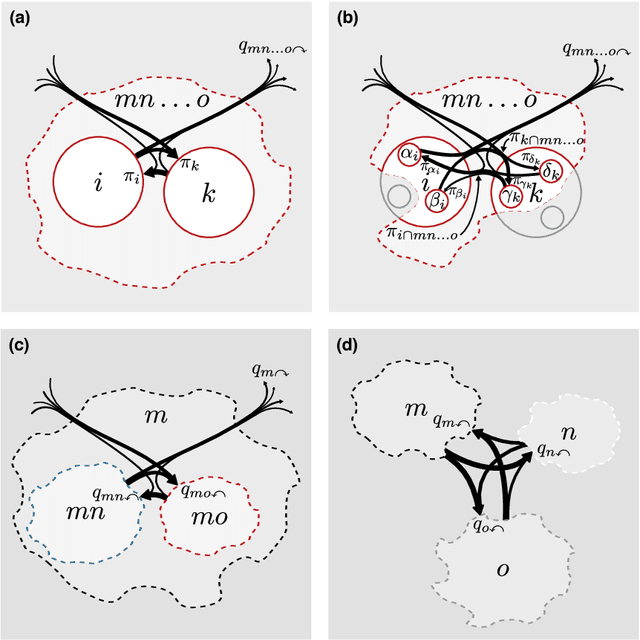
Comprehending complex systems by simplifying and highlighting important dynamical patterns requires modeling and mapping higher-order network flows. However, complex systems come in many forms and demand a range of representations, including memory and multilayer networks, which in turn call for versatile community-detection algorithms to reveal important modular regularities in the flows. Here we show that various forms of higher-order network flows can be represented in a unified way with networks that distinguish physical nodes for representing a~complex system's objects from state nodes for describing flows between the objects. Moreover, these so-called sparse memory networks allow the information-theoretic community detection method known as the map equation to identify overlapping and nested flow modules in data from a range of~different higher-order interactions such as multistep, multi-source, and temporal data. We derive the map equation applied to sparse memory networks and describe its search algorithm Infomap, which can exploit the flexibility of sparse memory networks. Together they provide a general solution to reveal overlapping modular patterns in higher-order flows through complex systems.