Cross-validation based Nonlinear Shrinkage

Many machine learning algorithms require precise estimates of covariance matrices. The sample covariance matrix performs poorly in high-dimensional settings, which has stimulated the development of alternative methods, the majority based on factor models and shrinkage. Recent work of Ledoit and Wolf has extended the shrinkage framework to Nonlinear Shrinkage (NLS), a more powerful covariance estimator based on Random Matrix Theory. Our contribution shows that, contrary to claims in the literature, cross-validation based covariance matrix estimation (CVC) yields comparable performance at strongly reduced complexity and runtime. On two real world data sets, we show that the CVC estimator yields superior results than competing shrinkage and factor based methods.

Validity of time reversal for testing Granger causality

Inferring causal interactions from observed data is a challenging problem, especially in the presence of measurement noise. To alleviate the problem of spurious causality, Haufe et al. (2013) proposed to contrast measures of information flow obtained on the original data against the same measures obtained on time-reversed data. They show that this procedure, time-reversed Granger causality (TRGC), robustly rejects causal interpretations on mixtures of independent signals. While promising results have been achieved in simulations, it was so far unknown whether time reversal leads to valid measures of information flow in the presence of true interaction. Here we prove that, for linear finite-order autoregressive processes with unidirectional information flow, the application of time reversal for testing Granger causality indeed leads to correct estimates of information flow and its directionality. Using simulations, we further show that TRGC is able to infer correct directionality with similar statistical power as the net Granger causality between two variables, while being much more robust to the presence of measurement noise.

Multi-Target Shrinkage

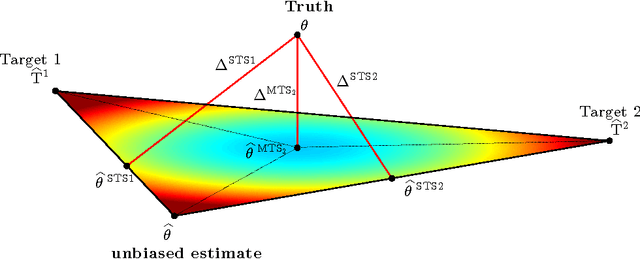
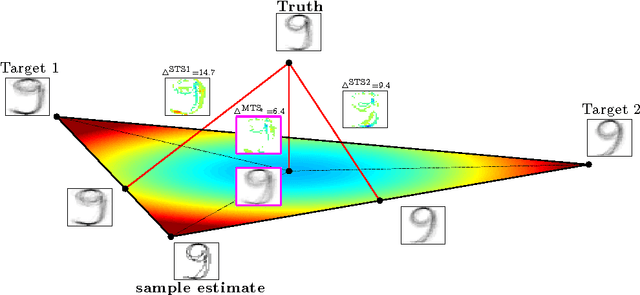
Stein showed that the multivariate sample mean is outperformed by "shrinking" to a constant target vector. Ledoit and Wolf extended this approach to the sample covariance matrix and proposed a multiple of the identity as shrinkage target. In a general framework, independent of a specific estimator, we extend the shrinkage concept by allowing simultaneous shrinkage to a set of targets. Application scenarios include settings with (A) additional data sets from potentially similar distributions, (B) non-stationarity, (C) a natural grouping of the data or (D) multiple alternative estimators which could serve as targets. We show that this Multi-Target Shrinkage can be translated into a quadratic program and derive conditions under which the estimation of the shrinkage intensities yields optimal expected squared error in the limit. For the sample mean and the sample covariance as specific instances, we derive conditions under which the optimality of MTS is applicable. We consider two asymptotic settings: the large dimensional limit (LDL), where the dimensionality and the number of observations go to infinity at the same rate, and the finite observations large dimensional limit (FOLDL), where only the dimensionality goes to infinity while the number of observations remains constant. We then show the effectiveness in extensive simulations and on real world data.