Comparison of Lightweight Methods for Vehicle Dynamics-Based Driver Drowsiness Detection

Driver drowsiness detection (DDD) prevents road accidents caused by driver fatigue. Vehicle dynamics-based DDD has been proposed as a method that is both economical and high performance. However, there are concerns about the reliability of performance metrics and the reproducibility of many of the existing methods. For instance, some previous studies seem to have a data leakage issue among training and test datasets, and many do not openly provide the datasets they used. To this end, this paper aims to compare the performance of representative vehicle dynamics-based DDD methods under a transparent and fair framework that uses a public dataset. We first develop a framework for extracting features from an open dataset by Aygun et al. and performing DDD with lightweight ML models; the framework is carefully designed to support a variety of onfigurations. Second, we implement three existing representative methods and a concise random forest (RF)-based method in the framework. Finally, we report the results of experiments to verify the reproducibility and clarify the performance of DDD based on common metrics. Among the evaluated methods, the RF-based method achieved the highest accuracy of 88 %. Our findings imply the issues inherent in DDD methods developed in a non-standard manner, and demonstrate a high performance method implemented appropriately.

Scalable Parallel Numerical Constraint Solver Using Global Load Balancing

We present a scalable parallel solver for numerical constraint satisfaction problems (NCSPs). Our parallelization scheme consists of homogeneous worker solvers, each of which runs on an available core and communicates with others via the global load balancing (GLB) method. The parallel solver is implemented with X10 that provides an implementation of GLB as a library. In experiments, several NCSPs from the literature were solved and attained up to 516-fold speedup using 600 cores of the TSUBAME2.5 supercomputer.

Scalable Parallel Numerical CSP Solver

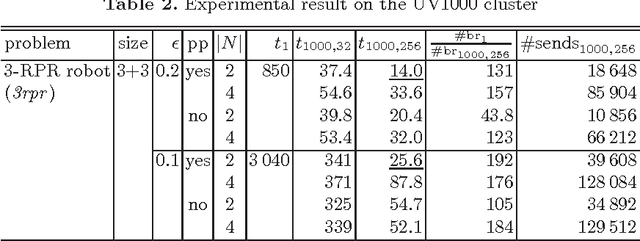
We present a parallel solver for numerical constraint satisfaction problems (NCSPs) that can scale on a number of cores. Our proposed method runs worker solvers on the available cores and simultaneously the workers cooperate for the search space distribution and balancing. In the experiments, we attained up to 119-fold speedup using 256 cores of a parallel computer.