SQuadMDS: a lean Stochastic Quartet MDS improving global structure preservation in neighbor embedding like t-SNE and UMAP

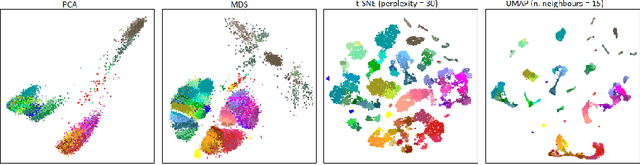
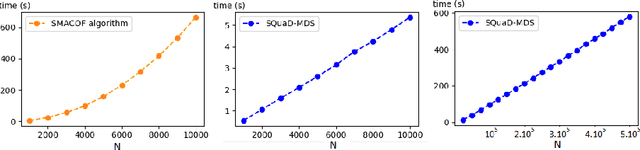
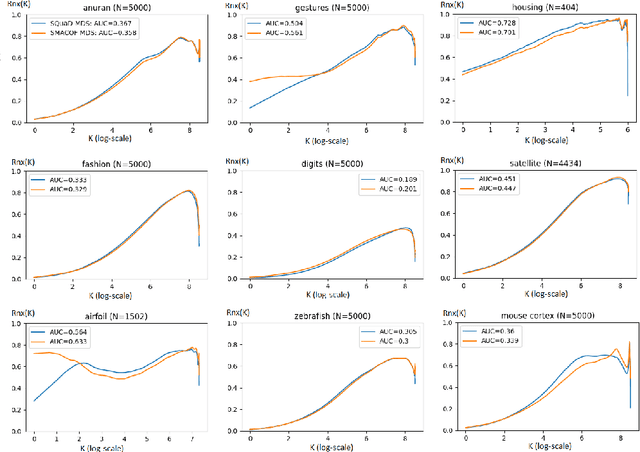
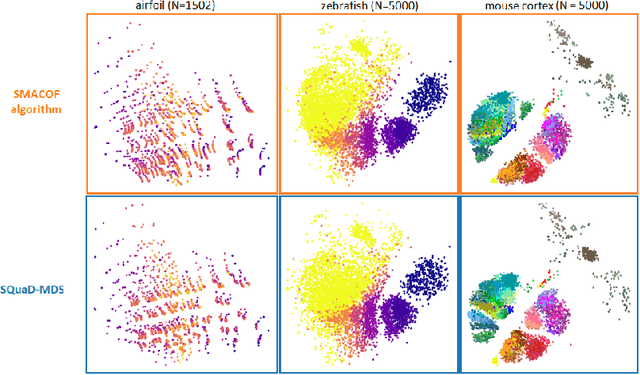
Multidimensional scaling is a statistical process that aims to embed high dimensional data into a lower-dimensional space; this process is often used for the purpose of data visualisation. Common multidimensional scaling algorithms tend to have high computational complexities, making them inapplicable on large data sets. This work introduces a stochastic, force directed approach to multidimensional scaling with a time and space complexity of O(N), with N data points. The method can be combined with force directed layouts of the family of neighbour embedding such as t-SNE, to produce embeddings that preserve both the global and the local structures of the data. Experiments assess the quality of the embeddings produced by the standalone version and its hybrid extension both quantitatively and qualitatively, showing competitive results outperforming state-of-the-art approaches. Codes are available at https://github.com/PierreLambert3/SQuaD-MDS-and-FItSNE-hybrid.

Perplexity-free Parametric t-SNE

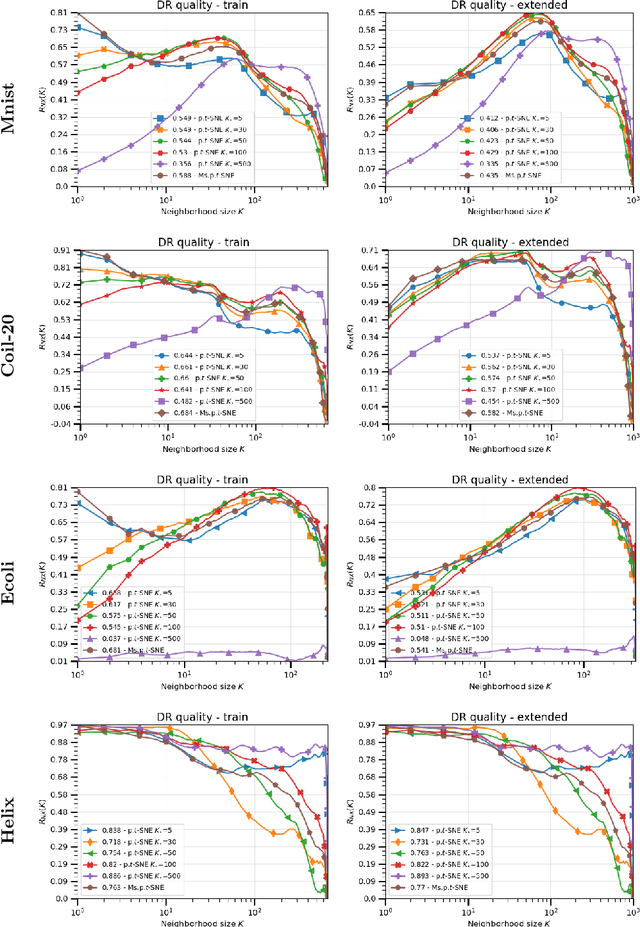
The t-distributed Stochastic Neighbor Embedding (t-SNE) algorithm is a ubiquitously employed dimensionality reduction (DR) method. Its non-parametric nature and impressive efficacy motivated its parametric extension. It is however bounded to a user-defined perplexity parameter, restricting its DR quality compared to recently developed multi-scale perplexity-free approaches. This paper hence proposes a multi-scale parametric t-SNE scheme, relieved from the perplexity tuning and with a deep neural network implementing the mapping. It produces reliable embeddings with out-of-sample extensions, competitive with the best perplexity adjustments in terms of neighborhood preservation on multiple data sets.