Cosimo Rubino
3D Pose from Detections
Jul 20, 2015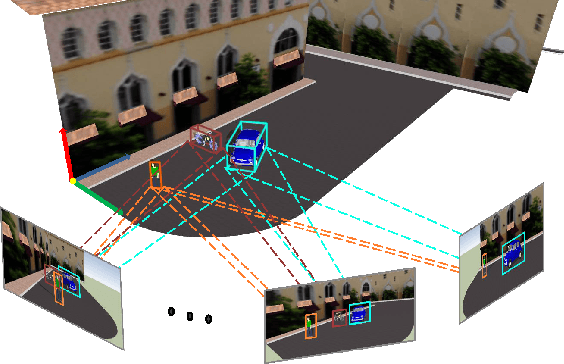


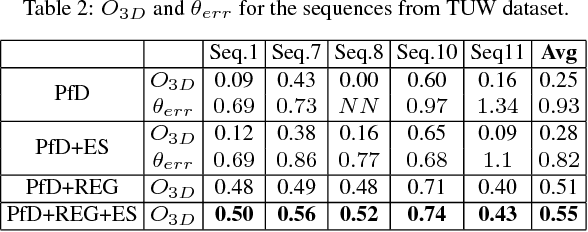
Abstract:We present a novel method to infer, in closed-form, a general 3D spatial occupancy and orientation of a collection of rigid objects given 2D image detections from a sequence of images. In particular, starting from 2D ellipses fitted to bounding boxes, this novel multi-view problem can be reformulated as the estimation of a quadric (ellipsoid) in 3D. We show that an efficient solution exists in the dual-space using a minimum of three views while a solution with two views is possible through the use of regularization. However, this algebraic solution can be negatively affected in the presence of gross inaccuracies in the bounding boxes estimation. To this end, we also propose a robust ellipse fitting algorithm able to improve performance in the presence of errors in the detected objects. Results on synthetic tests and on different real datasets, involving real challenging scenarios, demonstrate the applicability and potential of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge