cuSLINK: Single-linkage Agglomerative Clustering on the GPU

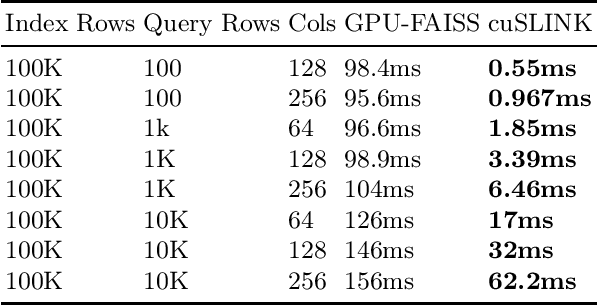
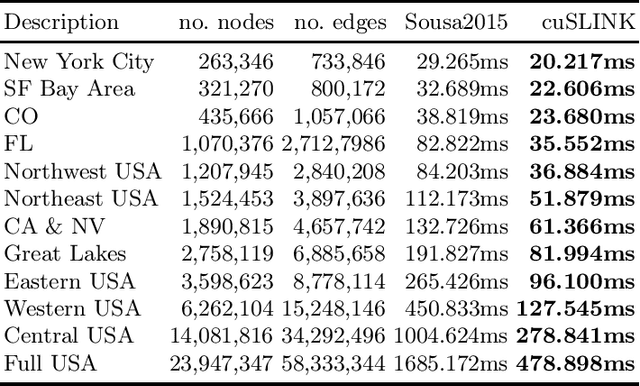
In this paper, we propose cuSLINK, a novel and state-of-the-art reformulation of the SLINK algorithm on the GPU which requires only $O(Nk)$ space and uses a parameter $k$ to trade off space and time. We also propose a set of novel and reusable building blocks that compose cuSLINK. These building blocks include highly optimized computational patterns for $k$-NN graph construction, spanning trees, and dendrogram cluster extraction. We show how we used our primitives to implement cuSLINK end-to-end on the GPU, further enabling a wide range of real-world data mining and machine learning applications that were once intractable. In addition to being a primary computational bottleneck in the popular HDBSCAN algorithm, the impact of our end-to-end cuSLINK algorithm spans a large range of important applications, including cluster analysis in social and computer networks, natural language processing, and computer vision. Users can obtain cuSLINK at https://docs.rapids.ai/api/cuml/latest/api/#agglomerative-clustering

Semiring Primitives for Sparse Neighborhood Methods on the GPU

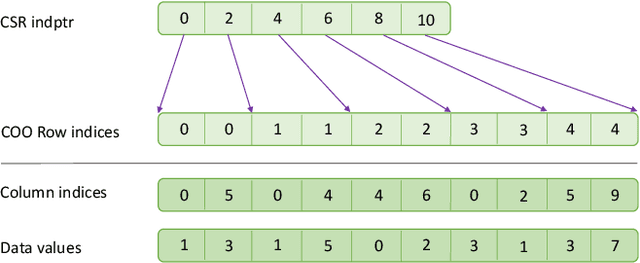
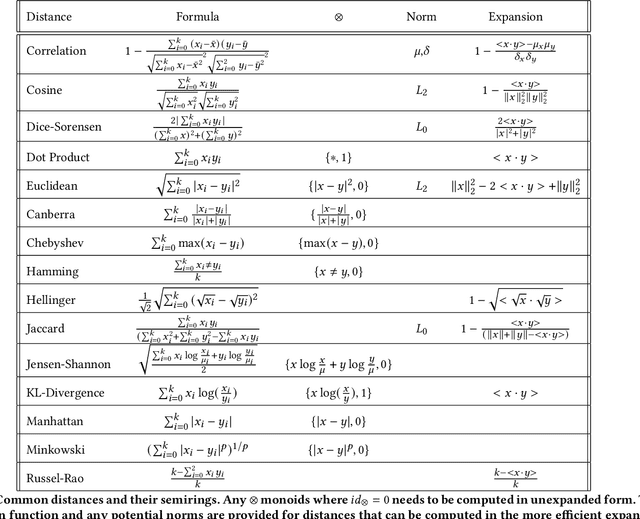
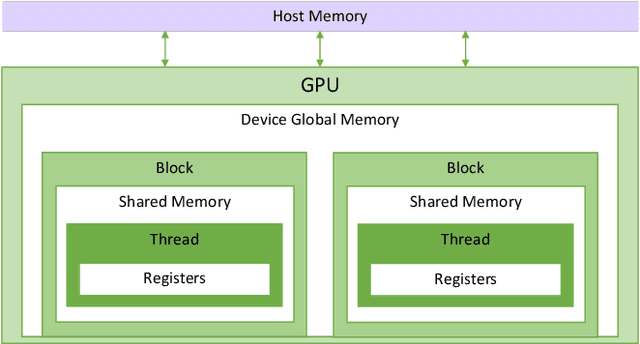
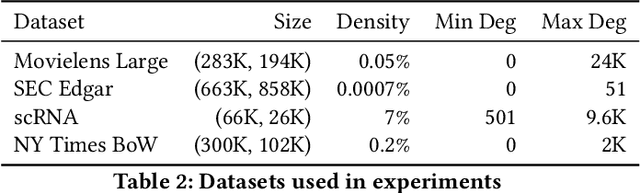
High-performance primitives for mathematical operations on sparse vectors must deal with the challenges of skewed degree distributions and limits on memory consumption that are typically not issues in dense operations. We demonstrate that a sparse semiring primitive can be flexible enough to support a wide range of critical distance measures while maintaining performance and memory efficiency on the GPU. We further show that this primitive is a foundational component for enabling many neighborhood-based information retrieval and machine learning algorithms to accept sparse input. To our knowledge, this is the first work aiming to unify the computation of several critical distance measures on the GPU under a single flexible design paradigm and we hope that it provides a good baseline for future research in this area. Our implementation is fully open source and publicly available at https://github.com/rapidsai/cuml.

Bringing UMAP Closer to the Speed of Light with GPU Acceleration

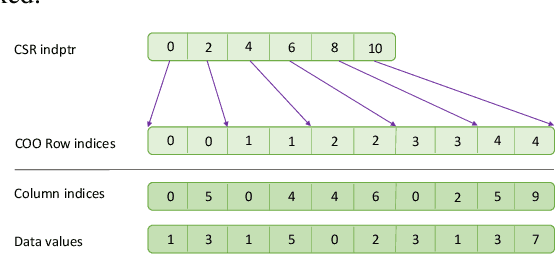
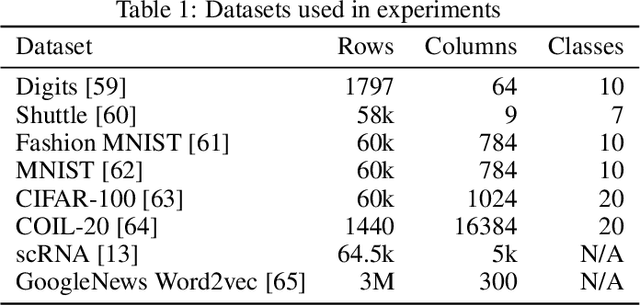
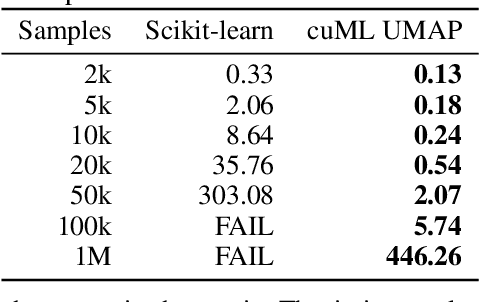
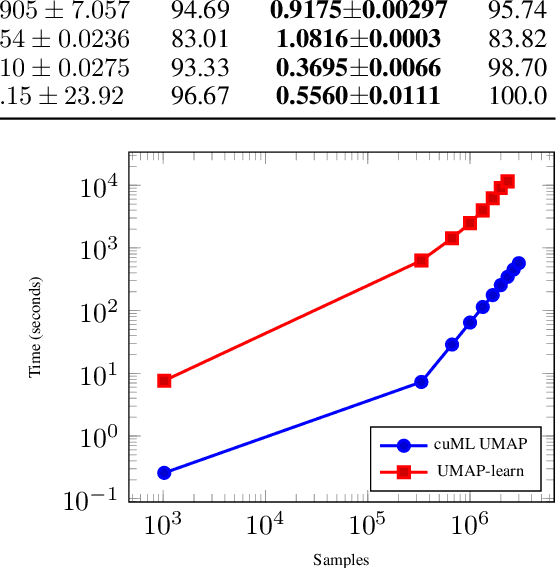
The Uniform Manifold Approximation and Projection (UMAP) algorithm has become widely popular for its ease of use, quality of results, and support for exploratory, unsupervised, supervised, and semi-supervised learning. While many algorithms can be ported to a GPU in a simple and direct fashion, such efforts have resulted in inefficent and inaccurate versions of UMAP. We show a number of techniques that can be used to make a faster and more faithful GPU version of UMAP, and obtain speedups of up to 100x in practice. Many of these design choices/lessons are general purpose and may inform the conversion of other graph and manifold learning algorithms to use GPUs. Our implementation has been made publicly available as part of the open source RAPIDS cuML library(https://github.com/rapidsai/cuml).