Necessary and Sufficient Conditions for Surrogate Functions of Pareto Frontiers and Their Synthesis Using Gaussian Processes

This paper introduces the necessary and sufficient conditions that surrogate functions must satisfy to properly define frontiers of non-dominated solutions in multi-objective optimization problems. These new conditions work directly on the objective space, thus being agnostic about how the solutions are evaluated. Therefore, real objectives or user-designed objectives' surrogates are allowed, opening the possibility of linking independent objective surrogates. To illustrate the practical consequences of adopting the proposed conditions, we use Gaussian processes as surrogates endowed with monotonicity soft constraints and with an adjustable degree of flexibility, and compare them to regular Gaussian processes and to a frontier surrogate method in the literature that is the closest to the method proposed in this paper. Results show that the necessary and sufficient conditions proposed here are finely managed by the constrained Gaussian process, guiding to high-quality surrogates capable of suitably synthesizing an approximation to the Pareto frontier in challenging instances of multi-objective optimization, while an existing approach that does not take the theory proposed in consideration defines surrogates which greatly violate the conditions to describe a valid frontier.

Multi-Objective Optimization for Self-Adjusting Weighted Gradient in Machine Learning Tasks

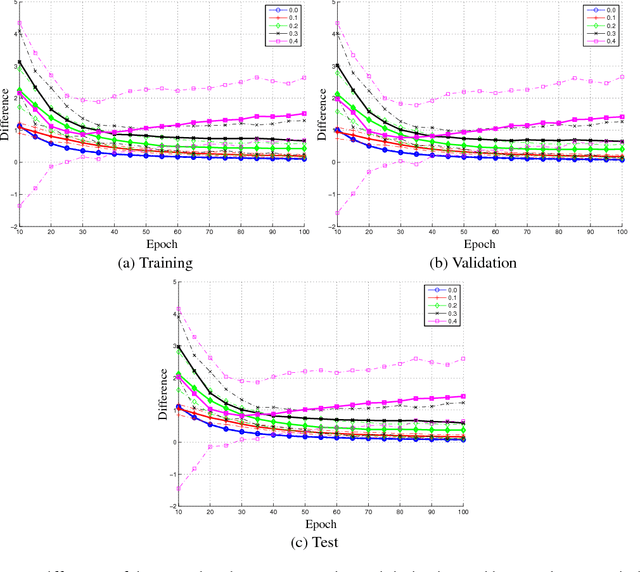
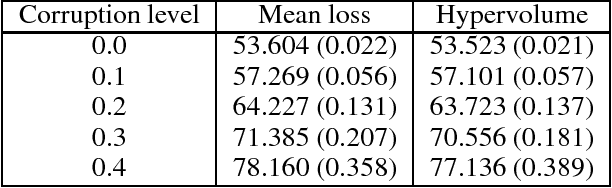
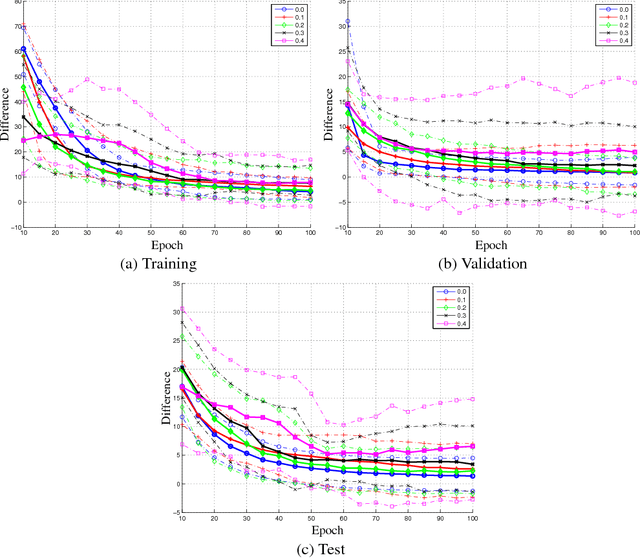
Much of the focus in machine learning research is placed in creating new architectures and optimization methods, but the overall loss function is seldom questioned. This paper interprets machine learning from a multi-objective optimization perspective, showing the limitations of the default linear combination of loss functions over a data set and introducing the hypervolume indicator as an alternative. It is shown that the gradient of the hypervolume is defined by a self-adjusting weighted mean of the individual loss gradients, making it similar to the gradient of a weighted mean loss but without requiring the weights to be defined a priori. This enables an inner boosting-like behavior, where the current model is used to automatically place higher weights on samples with higher losses but without requiring the use of multiple models. Results on a denoising autoencoder show that the new formulation is able to achieve better mean loss than the direct optimization of the mean loss, providing evidence to the conjecture that self-adjusting the weights creates a smoother loss surface.

Hybrid Algorithm for Multi-Objective Optimization by Greedy Hypervolume Maximization

This paper introduces a high-performance hybrid algorithm, called Hybrid Hypervolume Maximization Algorithm (H2MA), for multi-objective optimization that alternates between exploring the decision space and exploiting the already obtained non-dominated solutions. The proposal is centered on maximizing the hypervolume indicator, thus converting the multi-objective problem into a single-objective one. The exploitation employs gradient-based methods, but considering a single candidate efficient solution at a time, to overcome limitations associated with population-based approaches and also to allow an easy control of the number of solutions provided. There is an interchange between two steps. The first step is a deterministic local exploration, endowed with an automatic procedure to detect stagnation. When stagnation is detected, the search is switched to a second step characterized by a stochastic global exploration using an evolutionary algorithm. Using five ZDT benchmarks with 30 variables, the performance of the new algorithm is compared to state-of-the-art algorithms for multi-objective optimization, more specifically NSGA-II, SPEA2, and SMS-EMOA. The solutions found by the H2MA guide to higher hypervolume and smaller distance to the true Pareto frontier with significantly less function evaluations, even when the gradient is estimated numerically. Furthermore, although only continuous decision spaces have been considered here, discrete decision spaces could also have been treated, replacing gradient-based search by hill-climbing. Finally, a thorough explanation is provided to support the expressive gain in performance that was achieved.