Naive Algorithmic Collusion: When Do Bandit Learners Cooperate and When Do They Compete?

Algorithmic agents are used in a variety of competitive decision settings, notably in making pricing decisions in contexts that range from online retail to residential home rentals. Business managers, algorithm designers, legal scholars, and regulators alike are all starting to consider the ramifications of "algorithmic collusion." We study the emergent behavior of multi-armed bandit machine learning algorithms used in situations where agents are competing, but they have no information about the strategic interaction they are engaged in. Using a general-form repeated Prisoner's Dilemma game, agents engage in online learning with no prior model of game structure and no knowledge of competitors' states or actions (e.g., no observation of competing prices). We show that these context-free bandits, with no knowledge of opponents' choices or outcomes, still will consistently learn collusive behavior - what we call "naive collusion." We primarily study this system through an analytical model and examine perturbations to the model through simulations. Our findings have several notable implications for regulators. First, calls to limit algorithms from conditioning on competitors' prices are insufficient to prevent algorithmic collusion. This is a direct result of collusion arising even in the naive setting. Second, symmetry in algorithms can increase collusion potential. This highlights a new, simple mechanism for "hub-and-spoke" algorithmic collusion. A central distributor need not imbue its algorithm with supra-competitive tendencies for apparent collusion to arise; it can simply arise by using certain (common) machine learning algorithms. Finally, we highlight that collusive outcomes depend starkly on the specific algorithm being used, and we highlight market and algorithmic conditions under which it will be unknown a priori whether collusion occurs.

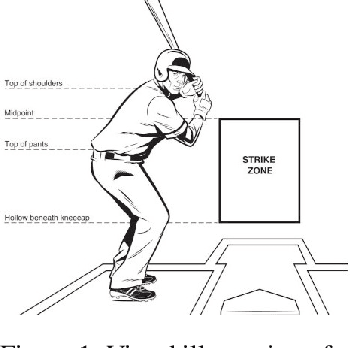
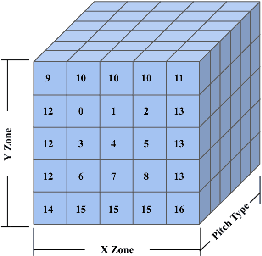
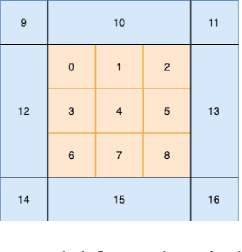
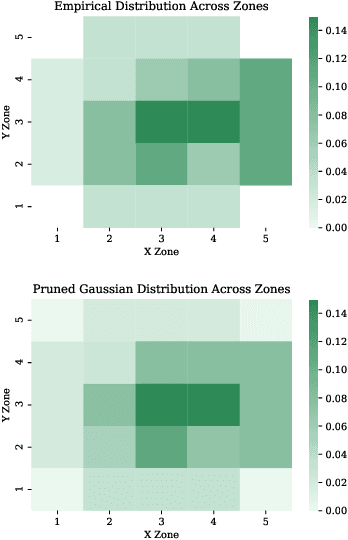
Computing an Optimal Pitching Strategy in a Baseball At-Bat

The field of quantitative analytics has transformed the world of sports over the last decade. To date, these analytic approaches are statistical at their core, characterizing what is and what was, while using this information to drive decisions about what to do in the future. However, as we often view team sports, such as soccer, hockey, and baseball, as pairwise win-lose encounters, it seems natural to model these as zero-sum games. We propose such a model for one important class of sports encounters: a baseball at-bat, which is a matchup between a pitcher and a batter. Specifically, we propose a novel model of this encounter as a zero-sum stochastic game, in which the goal of the batter is to get on base, an outcome the pitcher aims to prevent. The value of this game is the on-base percentage (i.e., the probability that the batter gets on base). In principle, this stochastic game can be solved using classical approaches. The main technical challenges lie in predicting the distribution of pitch locations as a function of pitcher intention, predicting the distribution of outcomes if the batter decides to swing at a pitch, and characterizing the level of patience of a particular batter. We address these challenges by proposing novel pitcher and batter representations as well as a novel deep neural network architecture for outcome prediction. Our experiments using Kaggle data from the 2015 to 2018 Major League Baseball seasons demonstrate the efficacy of the proposed approach.