AlphaZero Neural Scaling and Zipf's Law: a Tale of Board Games and Power Laws

Neural scaling laws are observed in a range of domains, to date with no clear understanding of why they occur. Recent theories suggest that loss power laws arise from Zipf's law, a power law observed in domains like natural language. One theory suggests that language scaling laws emerge when Zipf-distributed task quanta are learned in descending order of frequency. In this paper we examine power-law scaling in AlphaZero, a reinforcement learning algorithm, using a theory of language-model scaling. We find that game states in training and inference data scale with Zipf's law, which is known to arise from the tree structure of the environment, and examine the correlation between scaling-law and Zipf's-law exponents. In agreement with quanta scaling theory, we find that agents optimize state loss in descending order of frequency, even though this order scales inversely with modelling complexity. We also find that inverse scaling, the failure of models to improve with size, is correlated with unusual Zipf curves where end-game states are among the most frequent states. We show evidence that larger models shift their focus to these less-important states, sacrificing their understanding of important early-game states.

Climbing the Complexity Ladder with Expressive Attention

Attention involves comparing query and key vectors in terms of a scalar product, $\mathbf{Q}^T\mathbf{K}$, together with a subsequent softmax normalization. Classicaly, parallel/orthogonal/antiparallel queries and keys lead to large/intermediate/small attention weights. Here we study expressive attention (EA), which is based on $(\mathbf{Q}^T\mathbf{K})^2$, the squared dot product. In this case attention is enhanced when query and key are either parallel or antiparallel, and suppressed for orthogonal configurations. For a series of autoregressive prediction tasks, we find that EA performs at least as well as the standard mechanism, dot-product attention (DPA). Increasing task complexity, EA is observed to outperform DPA with increasing margins, which also holds for multi-task settings. For a given model size, EA manages to achieve 100\% performance for a range of complexity levels not accessible to DPA.

Scaling Laws for a Multi-Agent Reinforcement Learning Model

The recent observation of neural power-law scaling relations has made a significant impact in the field of deep learning. A substantial amount of attention has been dedicated as a consequence to the description of scaling laws, although mostly for supervised learning and only to a reduced extent for reinforcement learning frameworks. In this paper we present an extensive study of performance scaling for a cornerstone reinforcement learning algorithm, AlphaZero. On the basis of a relationship between Elo rating, playing strength and power-law scaling, we train AlphaZero agents on the games Connect Four and Pentago and analyze their performance. We find that player strength scales as a power law in neural network parameter count when not bottlenecked by available compute, and as a power of compute when training optimally sized agents. We observe nearly identical scaling exponents for both games. Combining the two observed scaling laws we obtain a power law relating optimal size to compute similar to the ones observed for language models. We find that the predicted scaling of optimal neural network size fits our data for both games. This scaling law implies that previously published state-of-the-art game-playing models are significantly smaller than their optimal size, given the respective compute budgets. We also show that large AlphaZero models are more sample efficient, performing better than smaller models with the same amount of training data.

Emotions as abstract evaluation criteria in biological and artificial intelligences

Biological as well as advanced artificial intelligences (AIs) need to decide which goals to pursue. We review nature's solution to the time allocation problem, which is based on a continuously readjusted categorical weighting mechanism we experience introspectively as emotions. One observes phylogenetically that the available number of emotional states increases hand in hand with the cognitive capabilities of animals and that raising levels of intelligence entail ever larger sets of behavioral options. Our ability to experience a multitude of potentially conflicting feelings is in this view not a leftover of a more primitive heritage, but a generic mechanism for attributing values to behavioral options that can not be specified at birth. In this view, emotions are essential for understanding the mind. For concreteness, we propose and discuss a framework which mimics emotions on a functional level. Based on time allocation via emotional stationarity (TAES), emotions are implemented as abstract criteria, such as satisfaction, challenge and boredom, which serve to evaluate activities that have been carried out. The resulting timeline of experienced emotions is compared with the `character' of the agent, which is defined in terms of a preferred distribution of emotional states. The long-term goal of the agent, to align experience with character, is achieved by optimizing the frequency for selecting individual tasks. Upon optimization, the statistics of emotion experience becomes stationary.

Investment vs. reward in a competitive knapsack problem

Natural selection drives species to develop brains, with sizes that increase with the complexity of the tasks to be tackled. Our goal is to investigate the balance between the metabolic costs of larger brains compared to the advantage they provide in solving general and combinatorial problems. Defining advantage as the performance relative to competitors, a two-player game based on the knapsack problem is used. Within this framework, two opponents compete over shared resources, with the goal of collecting more resources than the opponent. Neural nets of varying sizes are trained using a variant of the AlphaGo Zero algorithm. A surprisingly simple relation, $N_A/(N_A+N_B)$, is found for the relative win rate of a net with $N_A$ neurons against one with $N_B$. Success increases linearly with investments in additional resources when the networks sizes are very different, i.e. when $N_A \ll N_B$, with returns diminishing when both networks become comparable in size.

A generic framework for task selection driven by synthetic emotions

Given a certain complexity level, humanized agents may select from a wide range of possible tasks, with each activity corresponding to a transient goal. In general there will be no overarching credit assignment scheme allowing to compare available options with respect to expected utilities. For this situation we propose a task selection framework that is based on time allocation via emotional stationarity (TAES). Emotions are argued to correspond to abstract criteria, such as satisfaction, challenge and boredom, along which activities that have been carried out can be evaluated. The resulting timeline of experienced emotions is then compared with the `character' of the agent, which is defined in terms of a preferred distribution of emotional states. The long-term goal of the agent, to align experience with character, is achieved by optimizing the frequency for selecting the individual tasks. Upon optimization, the statistics of emotion experience becomes stationary.

When the goal is to generate a series of activities: A self-organized simulated robot arm

Behavior is characterized by sequences of goal-oriented conducts, such as food uptake, socializing and resting. Classically, one would define for each task a corresponding satisfaction level, with the agent engaging, at a given time, in the activity having the lowest satisfaction level. Alternatively, one may consider that the agent follows the overarching objective to generate sequences of distinct activities. To achieve a balanced distribution of activities would then be the primary goal, and not to master a specific task. In this setting, the agent would show two types of behaviors, task-oriented, and task-searching phases, with the latter interseeding the former. We study the emergence of autonomous task switching for the case of a simulated robot arm. Grasping one of several moving objects corresponds in this setting to a specific activity. Overall, the arm should follow a given object temporarily and then move away, in order to search for a new target and reengage. We show that this behavior can be generated robustly when modeling the arm as an adaptive dynamical system. The dissipation function is in this approach time dependent. The arm is in a dissipative state when searching for a nearby object, dissipating energy on approach. Once close, the dissipation function starts to increase, with the eventual sign change implying that the arm will take up energy and wander off. The resulting explorative state ends when the dissipation function becomes again negative and the arm selects a new target. We believe that our approach may be generalized to generate self-organized sequences of activities in general.

Kick control: using the attracting states arising within the sensorimotor loop of self-organized robots as motor primitives

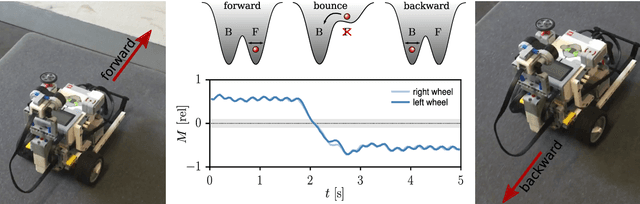
Self-organized robots may develop attracting states within the sensorimotor loop, that is within the phase space of neural activity, body, and environmental variables. Fixpoints, limit cycles, and chaotic attractors correspond in this setting to a non-moving robot, to directed, and to irregular locomotion respectively. Short higher-order control commands may hence be used to kick the system from one self-organized attractor robustly into the basin of attraction of a different attractor, a concept termed here as kick control. The individual sensorimotor states serve in this context as highly compliant motor primitives. We study different implementations of kick control for the case of simulated and real-world wheeled robots, for which the dynamics of the distinct wheels is generated independently by local feedback loops. The feedback loops are mediated by rate-encoding neurons disposing exclusively of propriosensoric inputs in terms of projections of the actual rotational angle of the wheel. The changes of the neural activity are then transmitted into a rotational motion by a simulated transmission rod akin to the transmission rods used for steam locomotives. We find that the self-organized attractor landscape may be morphed both by higher-level control signals, in the spirit of kick control, and by interacting with the environment. Bumping against a wall destroys the limit cycle corresponding to forward motion, with the consequence that the dynamical variables are then attracted in phase space by the limit cycle corresponding to backward moving. The robot, which does not dispose of any distance or contact sensors, hence reverses direction autonomously.

Closed-loop robots driven by short-term synaptic plasticity: Emergent explorative vs. limit-cycle locomotion

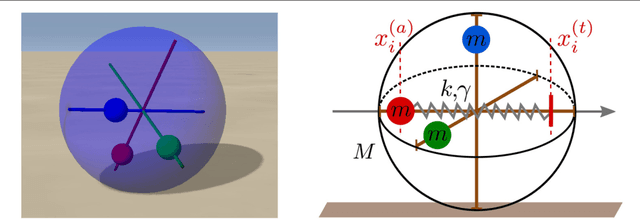
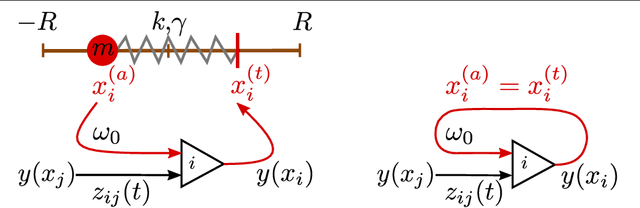
We examine the hypothesis, that short-term synaptic plasticity (STSP) may generate self-organized motor patterns. We simulated sphere-shaped autonomous robots, within the LPZRobots simulation package, containing three weights moving along orthogonal internal rods. The position of a weight is controlled by a single neuron receiving excitatory input from the sensor, measuring its actual position, and inhibitory inputs from the other two neurons. The inhibitory connections are transiently plastic, following physiologically inspired STSP-rules. We find that a wide palette of motion patterns are generated through the interaction of STSP, robot, and environment (closed-loop configuration), including various forward meandering and circular motions, together with chaotic trajectories. The observed locomotion is robust with respect to additional interactions with obstacles. In the chaotic phase the robot is seemingly engaged in actively exploring its environment. We believe that our results constitute a concept of proof that transient synaptic plasticity, as described by STSP, may potentially be important for the generation of motor commands and for the emergence of complex locomotion patterns, adapting seamlessly also to unexpected environmental feedback. We observe spontaneous and collision induced mode switchings, finding in addition, that locomotion may follow transiently limit cycles which are otherwise unstable. Regular locomotion corresponds to stable limit cycles in the sensorimotor loop, which may be characterized in turn by arbitrary angles of propagation. This degeneracy is, in our analysis, one of the drivings for the chaotic wandering observed for selected parameter settings, which is induced by the smooth diffusion of the angle of propagation.

The sensorimotor loop as a dynamical system: How regular motion primitives may emerge from self-organized limit cycles

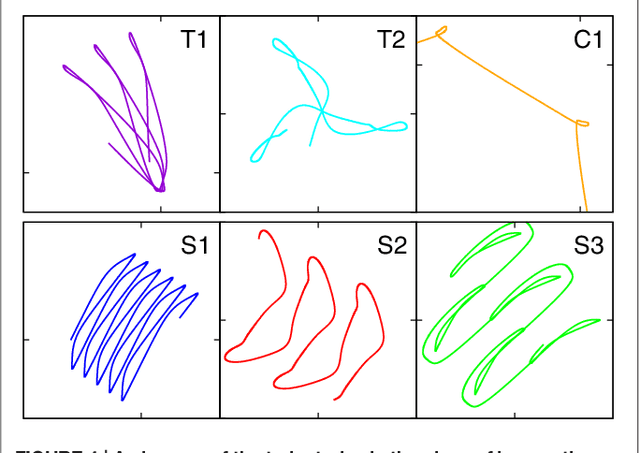
We investigate the sensorimotor loop of simple robots simulated within the LPZRobots environment from the point of view of dynamical systems theory. For a robot with a cylindrical shaped body and an actuator controlled by a single proprioceptual neuron we find various types of periodic motions in terms of stable limit cycles. These are self-organized in the sense, that the dynamics of the actuator kicks in only, for a certain range of parameters, when the barrel is already rolling, stopping otherwise. The stability of the resulting rolling motions terminates generally, as a function of the control parameters, at points where fold bifurcations of limit cycles occur. We find that several branches of motion types exist for the same parameters, in terms of the relative frequencies of the barrel and of the actuator, having each their respective basins of attractions in terms of initial conditions. For low drivings stable limit cycles describing periodic and drifting back-and-forth motions are found additionally. These modes allow to generate symmetry breaking explorative behavior purely by the timing of an otherwise neutral signal with respect to the cyclic back-and-forth motion of the robot.