GRPO-LEAD: A Difficulty-Aware Reinforcement Learning Approach for Concise Mathematical Reasoning in Language Models

Recent advances in R1-like reasoning models leveraging Group Relative Policy Optimization (GRPO) have significantly improved the performance of language models on mathematical reasoning tasks. However, current GRPO implementations encounter critical challenges, including reward sparsity due to binary accuracy metrics, limited incentives for conciseness, and insufficient focus on complex reasoning tasks. To address these issues, we propose GRPO-LEAD, a suite of novel enhancements tailored for mathematical reasoning. Specifically, GRPO-LEAD introduces (1) a length-dependent accuracy reward to encourage concise and precise solutions, (2) an explicit penalty mechanism for incorrect answers to sharpen decision boundaries, and (3) a difficulty-aware advantage reweighting strategy that amplifies learning signals for challenging problems. Furthermore, we systematically examine the impact of model scale and supervised fine-tuning (SFT) strategies, demonstrating that larger-scale base models and carefully curated datasets significantly enhance reinforcement learning effectiveness. Extensive empirical evaluations and ablation studies confirm that GRPO-LEAD substantially mitigates previous shortcomings, resulting in language models that produce more concise, accurate, and robust reasoning across diverse mathematical tasks.

TAU: Modeling Temporal Consistency Through Temporal Attentive U-Net for PPG Peak Detection

Photoplethysmography (PPG) sensors have been widely used in consumer wearable devices to monitor heart rates (HR) and heart rate variability (HRV). Despite the prevalence, PPG signals can be contaminated by motion artifacts induced from daily activities. Existing approaches mainly use the amplitude information to perform PPG peak detection. However, these approaches cannot accurately identify peaks, since motion artifacts may bring random and significant amplitude variations. To improve the performance of PPG peak detection, the time information can be used. Specifically, heart rates exhibit temporal consistency that consecutive heartbeat intervals in a normal person can have limited variations. To leverage the temporal consistency, we propose the Temporal Attentive U-Net, i.e., TAU, to accurately detect peaks from PPG signals. In TAU, we design a time module that encodes temporal consistency in temporal embeddings. We integrate the amplitude information with temporal embeddings using the attention mechanism to estimate peak labels. Our experimental results show that TAU outperforms eleven baselines on heart rate estimation by more than 22.4%. Our TAU model achieves the best performance across various Signal-to-Noise Ratio (SNR) levels. Moreover, we achieve Pearson correlation coefficients higher than 0.9 (p < 0.01) on estimating HRV features from low-noise-level PPG signals.

Position Information Emerges in Causal Transformers Without Positional Encodings via Similarity of Nearby Embeddings

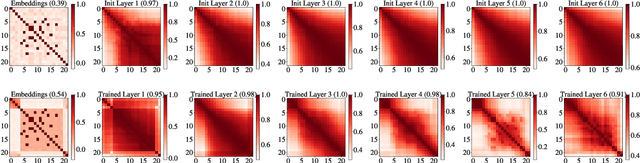
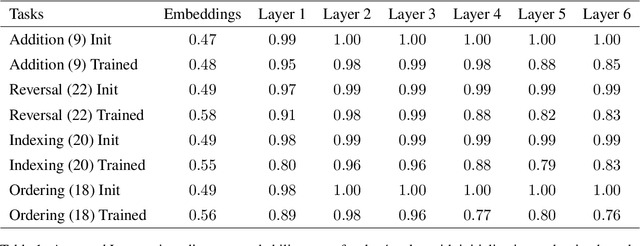
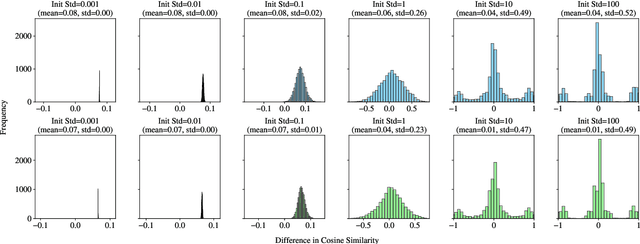
Transformers with causal attention can solve tasks that require positional information without using positional encodings. In this work, we propose and investigate a new hypothesis about how positional information can be stored without using explicit positional encoding. We observe that nearby embeddings are more similar to each other than faraway embeddings, allowing the transformer to potentially reconstruct the positions of tokens. We show that this pattern can occur in both the trained and the randomly initialized Transformer models with causal attention and no positional encodings over a common range of hyperparameters.

Breaking Symmetry When Training Transformers

As we show in this paper, the prediction for output token $n+1$ of Transformer architectures without one of the mechanisms of positional encodings and causal attention is invariant to permutations of input tokens $1, 2, ..., n-1$. Usually, both mechanisms are employed and the symmetry with respect to the input tokens is broken. Recently, it has been shown that one can train Transformers without positional encodings. This must be enabled by the causal attention mechanism. In this paper, we elaborate on the argument that the causal connection mechanism must be responsible for the fact that Transformers are able to model input sequences where the order is important. Vertical "slices" of Transformers are all encouraged to represent the same location $k$ in the input sequence. We hypothesize that residual connections contribute to this phenomenon, and demonstrate evidence for this.