CRUDE: Calibrating Regression Uncertainty Distributions Empirically

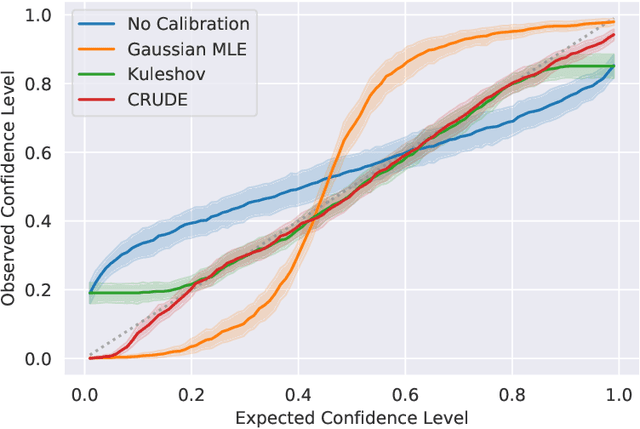
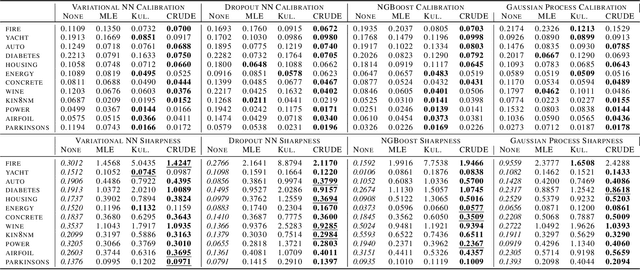
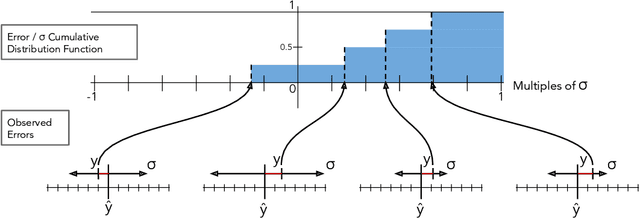
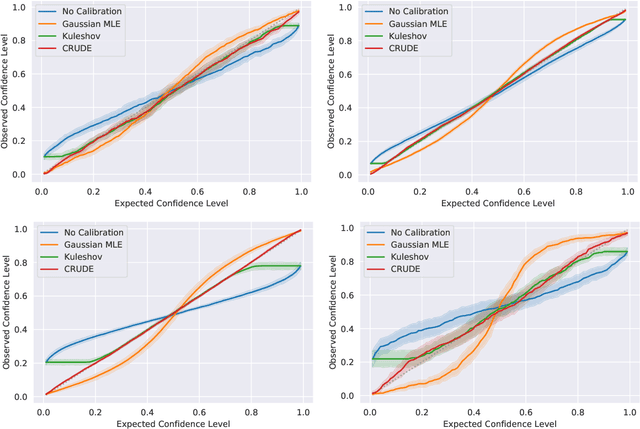
The importance of calibrated uncertainty estimates in machine learning is growing apparent across many fields such as autonomous vehicles, medicine, and weather and climate forecasting. While there is extensive literature on uncertainty calibration for classification, the classification findings do not always translate to regression. As a result, modern models for predicting uncertainty in regression settings typically produce uncalibrated and overconfident estimates. To address these gaps, we present a calibration method for regression settings that does not assume a particular uncertainty distribution over the error: Calibrating Regression Uncertainty Distributions Empirically (CRUDE). CRUDE makes the weaker assumption that error distributions have a constant arbitrary shape across the output space, shifted by predicted mean and scaled by predicted standard deviation. CRUDE requires no training of the calibration estimator, aside from a parameter to account for fixed bias in the predicted mean. Across an extensive set of regression tasks, CRUDE demonstrates consistently sharper, better calibrated, and more accurate uncertainty estimates than state-of-the-art techniques.