Christopher Hart
Leveraging directed causal discovery to detect latent common causes
Nov 11, 2019
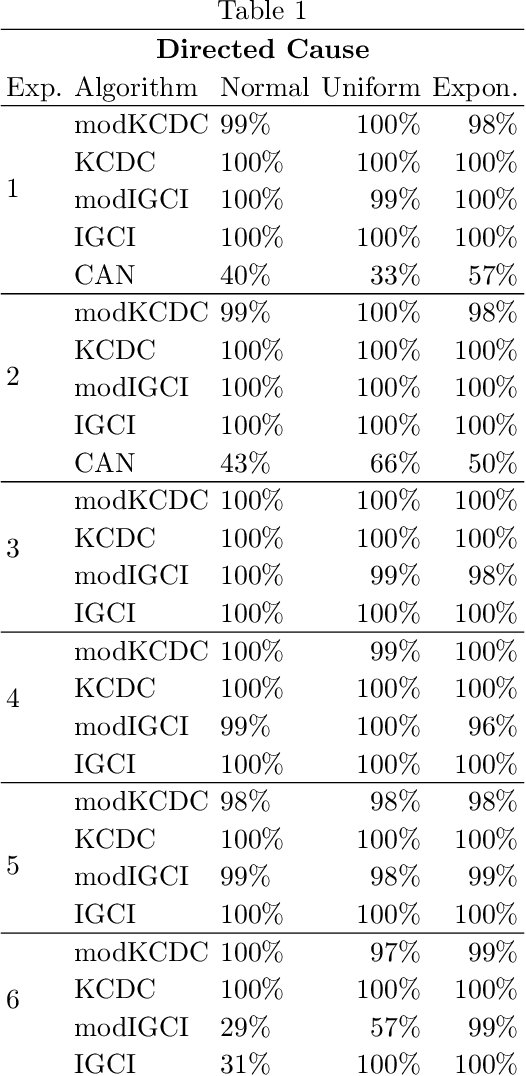


Abstract:The discovery of causal relationships is a fundamental problem in science and medicine. In recent years, many elegant approaches to discovering causal relationships between two variables from uncontrolled data have been proposed. However, most of these deal only with purely directed causal relationships and cannot detect latent common causes. Here, we devise a general method which takes a purely directed causal discovery algorithm and modifies it so that it can also detect latent common causes. The identifiability of the modified algorithm depends on the identifiability of the original, as well as an assumption that the strength of noise be relatively small. We apply our method to two directed causal discovery algorithms, the Information Geometric Causal Inference of (Daniusis et al., 2010) and the Kernel Conditional Deviance for Causal Inference of (Mitrovic, Sejdinovic, and Teh, 2018), and extensively test on synthetic data---detecting latent common causes in additive, multiplicative and complex noise regimes---and on real data, where we are able to detect known common causes. In addition to detecting latent common causes, our experiments demonstrate that both modified algorithms preserve the performance of the original directed algorithm in distinguishing directed causal relations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge