The Complexity of Limited Belief Reasoning -- The Quantifier-Free Case

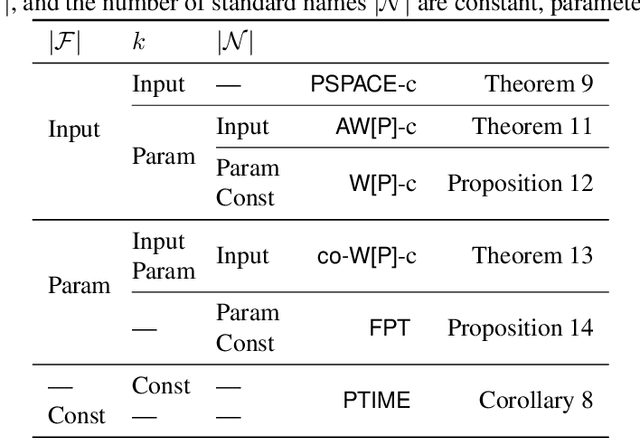
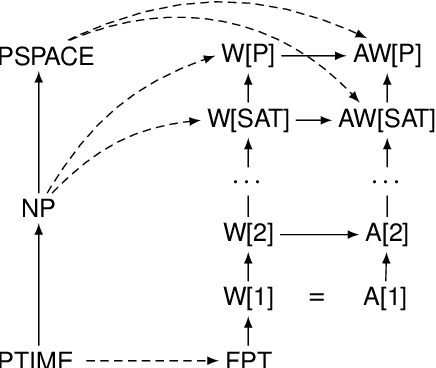
The classical view of epistemic logic is that an agent knows all the logical consequences of their knowledge base. This assumption of logical omniscience is often unrealistic and makes reasoning computationally intractable. One approach to avoid logical omniscience is to limit reasoning to a certain belief level, which intuitively measures the reasoning "depth." This paper investigates the computational complexity of reasoning with belief levels. First we show that while reasoning remains tractable if the level is constant, the complexity jumps to PSPACE-complete -- that is, beyond classical reasoning -- when the belief level is part of the input. Then we further refine the picture using parameterized complexity theory to investigate how the belief level and the number of non-logical symbols affect the complexity.

A Reasoning System for a First-Order Logic of Limited Belief

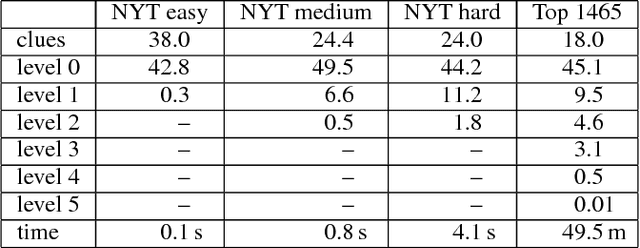
Logics of limited belief aim at enabling computationally feasible reasoning in highly expressive representation languages. These languages are often dialects of first-order logic with a weaker form of logical entailment that keeps reasoning decidable or even tractable. While a number of such logics have been proposed in the past, they tend to remain for theoretical analysis only and their practical relevance is very limited. In this paper, we aim to go beyond the theory. Building on earlier work by Liu, Lakemeyer, and Levesque, we develop a logic of limited belief that is highly expressive while remaining decidable in the first-order and tractable in the propositional case and exhibits some characteristics that make it attractive for an implementation. We introduce a reasoning system that employs this logic as representation language and present experimental results that showcase the benefit of limited belief.