The Complexity of Limited Belief Reasoning -- The Quantifier-Free Case
Paper and Code
May 08, 2018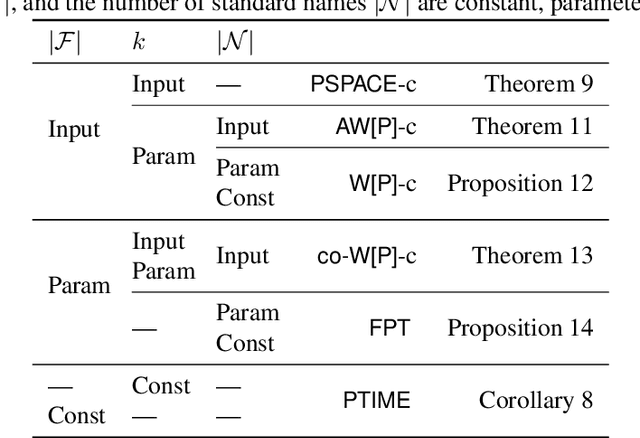
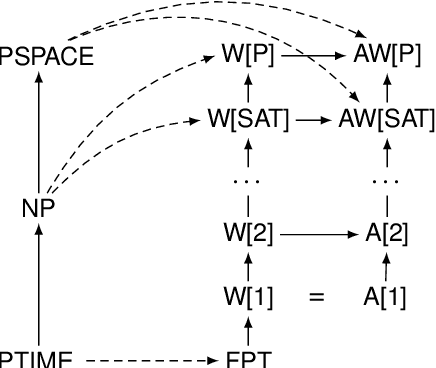
The classical view of epistemic logic is that an agent knows all the logical consequences of their knowledge base. This assumption of logical omniscience is often unrealistic and makes reasoning computationally intractable. One approach to avoid logical omniscience is to limit reasoning to a certain belief level, which intuitively measures the reasoning "depth." This paper investigates the computational complexity of reasoning with belief levels. First we show that while reasoning remains tractable if the level is constant, the complexity jumps to PSPACE-complete -- that is, beyond classical reasoning -- when the belief level is part of the input. Then we further refine the picture using parameterized complexity theory to investigate how the belief level and the number of non-logical symbols affect the complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge