Risk bounds for PU learning under Selected At Random assumption

Positive-unlabeled learning (PU learning) is known as a special case of semi-supervised binary classification where only a fraction of positive examples are labeled. The challenge is then to find the correct classifier despite this lack of information. Recently, new methodologies have been introduced to address the case where the probability of being labeled may depend on the covariates. In this paper, we are interested in establishing risk bounds for PU learning under this general assumption. In addition, we quantify the impact of label noise on PU learning compared to standard classification setting. Finally, we provide a lower bound on minimax risk proving that the upper bound is almost optimal.

A supervised clustering approach for fMRI-based inference of brain states

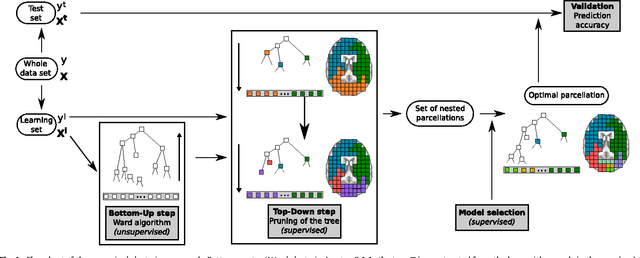
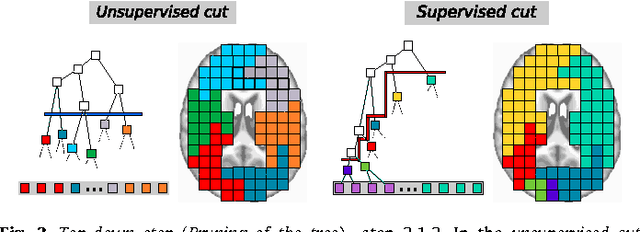
We propose a method that combines signals from many brain regions observed in functional Magnetic Resonance Imaging (fMRI) to predict the subject's behavior during a scanning session. Such predictions suffer from the huge number of brain regions sampled on the voxel grid of standard fMRI data sets: the curse of dimensionality. Dimensionality reduction is thus needed, but it is often performed using a univariate feature selection procedure, that handles neither the spatial structure of the images, nor the multivariate nature of the signal. By introducing a hierarchical clustering of the brain volume that incorporates connectivity constraints, we reduce the span of the possible spatial configurations to a single tree of nested regions tailored to the signal. We then prune the tree in a supervised setting, hence the name supervised clustering, in order to extract a parcellation (division of the volume) such that parcel-based signal averages best predict the target information. Dimensionality reduction is thus achieved by feature agglomeration, and the constructed features now provide a multi-scale representation of the signal. Comparisons with reference methods on both simulated and real data show that our approach yields higher prediction accuracy than standard voxel-based approaches. Moreover, the method infers an explicit weighting of the regions involved in the regression or classification task.