Christian Mendl
Quantum Policy Iteration via Amplitude Estimation and Grover Search -- Towards Quantum Advantage for Reinforcement Learning
Jun 09, 2022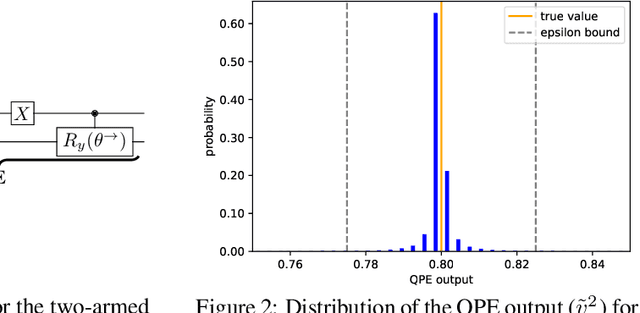
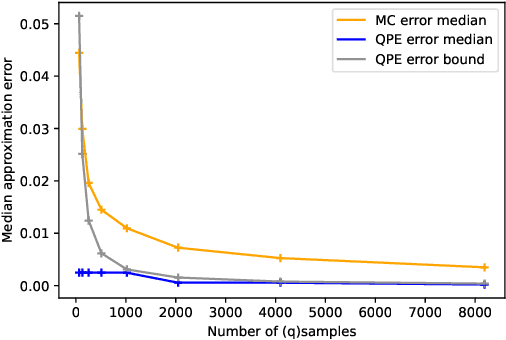
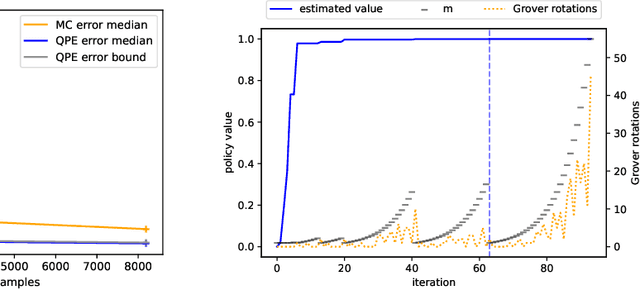
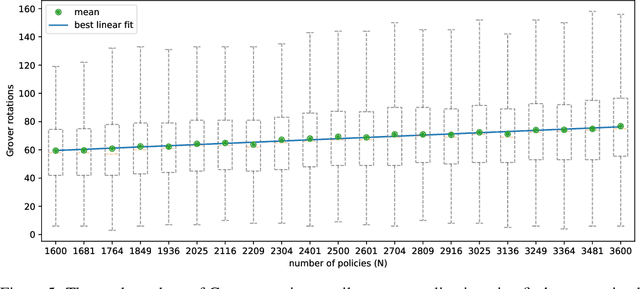
Abstract:We present a full implementation and simulation of a novel quantum reinforcement learning (RL) method and mathematically prove a quantum advantage. Our approach shows in detail how to combine amplitude estimation and Grover search into a policy evaluation and improvement scheme. We first develop quantum policy evaluation (QPE) which is quadratically more efficient compared to an analogous classical Monte Carlo estimation and is based on a quantum mechanical realization of a finite Markov decision process (MDP). Building on QPE, we derive a quantum policy iteration that repeatedly improves an initial policy using Grover search until the optimum is reached. Finally, we present an implementation of our algorithm for a two-armed bandit MDP which we then simulate. The results confirm that QPE provides a quantum advantage in RL problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge