SubsurfaceGen: Procedural Generation of Field-Scale Earth Models and Seismic Data

Full waveform inversion (FWI) is the gold standard for subsurface imaging, with applications from carbon sequestration to energy and mineral exploration to earthquake hazard assessment. Machine learning approaches to FWI need field-scale, geologically diverse, and physically realistic training data, but existing resources such as Marmousi, SEAM, and OpenFWI fall short on spatial extent, temporal extent, geological diversity, and physical realism. We address these limitations with SubsurfaceGen, a GPU-accelerated generator for 3D velocity models and seismic data. Along with SubsurfaceGen, we release a paired dataset of 4,276 2D velocity slices, 5 s wavefields, and 8 s shot gathers drawn from 42 realistic, field-scale 3D velocity models, each spanning 10 km x 10 km laterally and 6.19 km deep at 10 m resolution. The dataset spans six geological settings -- four built with SubsurfaceGen and two drawn from prior sources -- relevant for carbon sequestration and hydrocarbon exploration. We use this dataset to evaluate neural operators on wavefield prediction and encoder-decoders on end-to-end velocity inversion, holding out one geological setting for out-of-distribution testing. These experiments surface failure modes at field-scale and demonstrate how SubsurfaceGen and the associated dataset can impact ML-based FWI.

Spectrum-Informed Multistage Neural Networks: Multiscale Function Approximators of Machine Precision

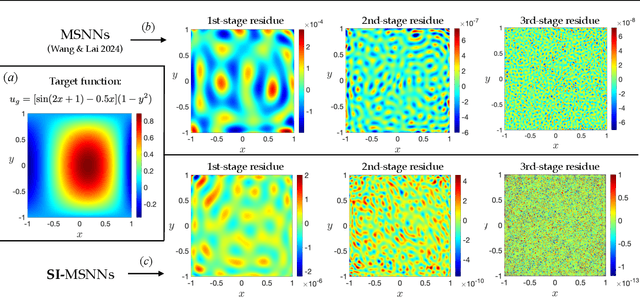
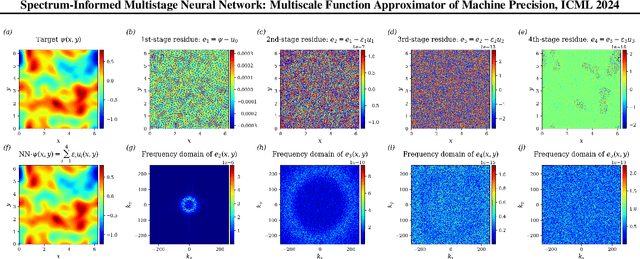
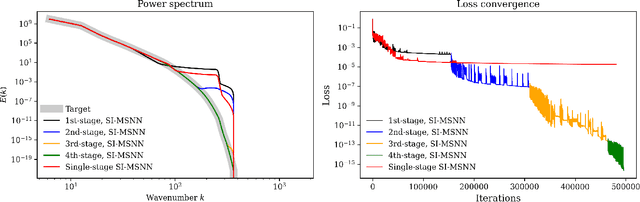
Deep learning frameworks have become powerful tools for approaching scientific problems such as turbulent flow, which has wide-ranging applications. In practice, however, existing scientific machine learning approaches have difficulty fitting complex, multi-scale dynamical systems to very high precision, as required in scientific contexts. We propose using the novel multistage neural network approach with a spectrum-informed initialization to learn the residue from the previous stage, utilizing the spectral biases associated with neural networks to capture high frequency features in the residue, and successfully tackle the spectral bias of neural networks. This approach allows the neural network to fit target functions to double floating-point machine precision $O(10^{-16})$.

Multi-stage Neural Networks: Function Approximator of Machine Precision

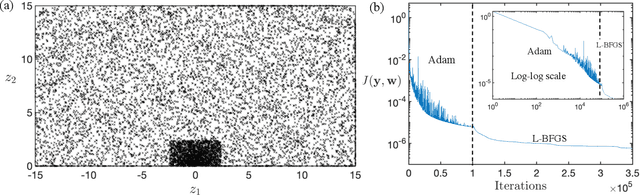
Deep learning techniques are increasingly applied to scientific problems, where the precision of networks is crucial. Despite being deemed as universal function approximators, neural networks, in practice, struggle to reduce the prediction errors below $O(10^{-5})$ even with large network size and extended training iterations. To address this issue, we developed the multi-stage neural networks that divides the training process into different stages, with each stage using a new network that is optimized to fit the residue from the previous stage. Across successive stages, the residue magnitudes decreases substantially and follows an inverse power-law relationship with the residue frequencies. The multi-stage neural networks effectively mitigate the spectral biases associated with regular neural networks, enabling them to capture the high frequency feature of target functions. We demonstrate that the prediction error from the multi-stage training for both regression problems and physics-informed neural networks can nearly reach the machine-precision $O(10^{-16})$ of double-floating point within a finite number of iterations. Such levels of accuracy are rarely attainable using single neural networks alone.

Self-similar blow-up profile for the Boussinesq equations via a physics-informed neural network

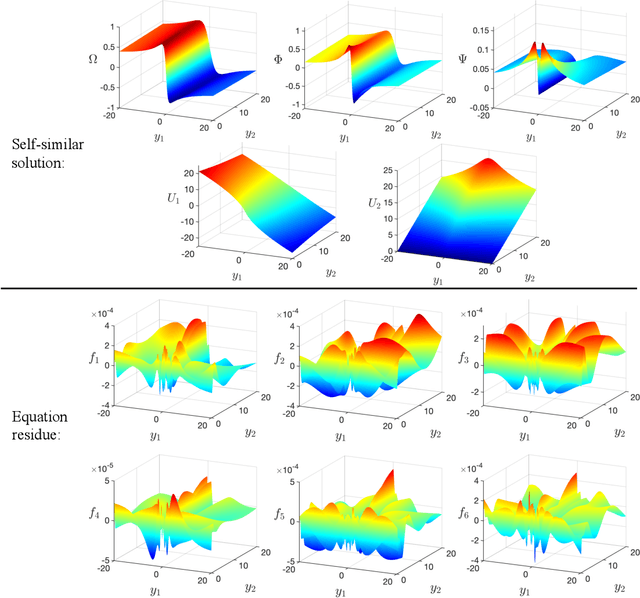
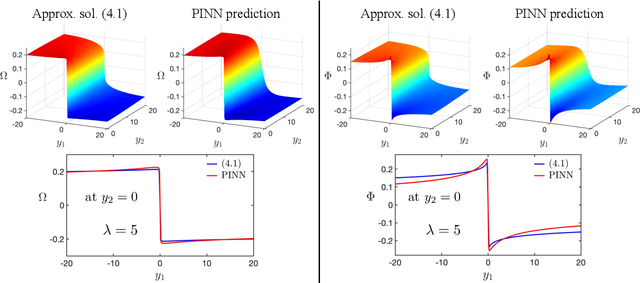
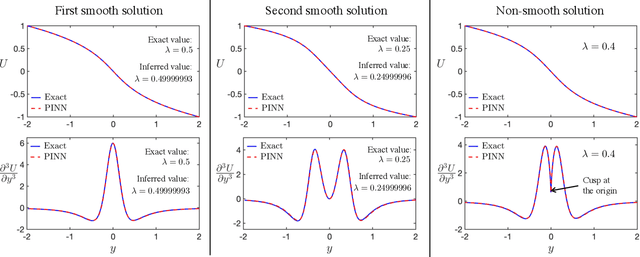
We develop a new numerical framework, employing physics-informed neural networks, to find a smooth self-similar solution for the Boussinesq equations. The solution in addition corresponds to an asymptotic self-similar profile for the 3-dimensional Euler equations in the presence of a cylindrical boundary. In particular, the solution represents a precise description of the Luo-Hou blow-up scenario [G. Luo, T. Hou, Proc. Natl. Acad. Sci. 111(36): 12968-12973, 2014] for 3-dimensional Euler. To the best of the authors' knowledge, the solution is the first truly multi-dimensional smooth backwards self-similar profile found for an equation from fluid mechanics. The new numerical framework is shown to be both robust and readily adaptable to other equations.