Self-similar blow-up profile for the Boussinesq equations via a physics-informed neural network
Paper and Code
Jan 18, 2022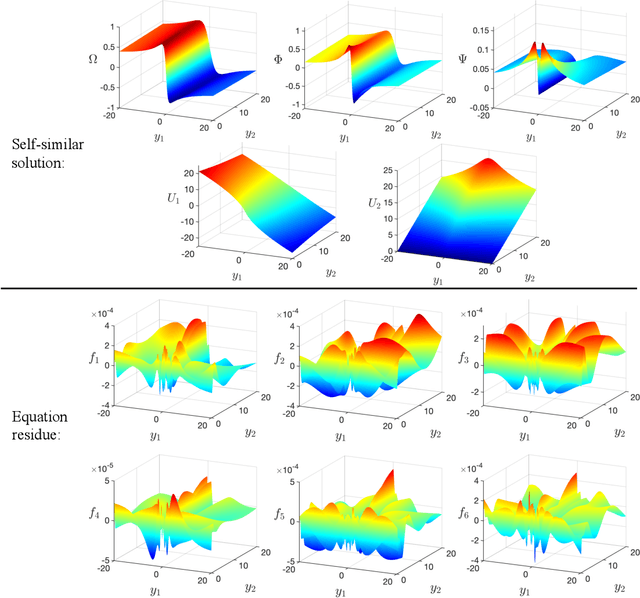
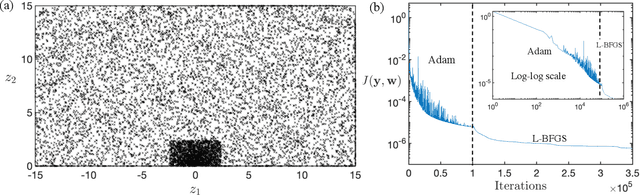
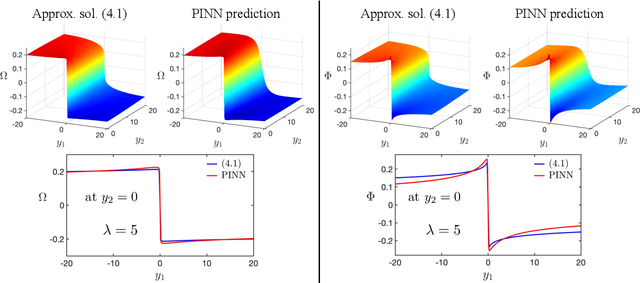
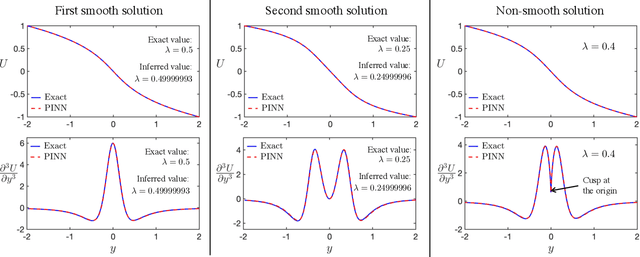
We develop a new numerical framework, employing physics-informed neural networks, to find a smooth self-similar solution for the Boussinesq equations. The solution in addition corresponds to an asymptotic self-similar profile for the 3-dimensional Euler equations in the presence of a cylindrical boundary. In particular, the solution represents a precise description of the Luo-Hou blow-up scenario [G. Luo, T. Hou, Proc. Natl. Acad. Sci. 111(36): 12968-12973, 2014] for 3-dimensional Euler. To the best of the authors' knowledge, the solution is the first truly multi-dimensional smooth backwards self-similar profile found for an equation from fluid mechanics. The new numerical framework is shown to be both robust and readily adaptable to other equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge