The Analysis from Nonlinear Distance Metric to Kernel-based Drug Prescription Prediction System

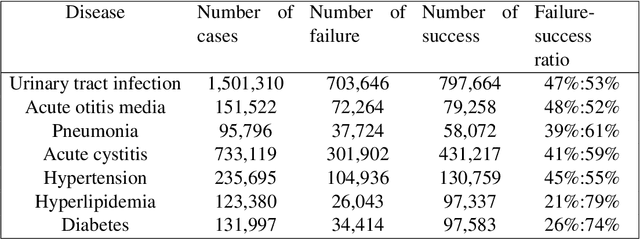
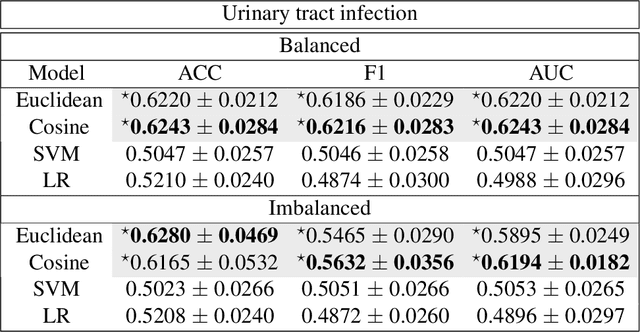
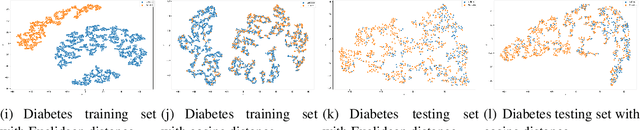
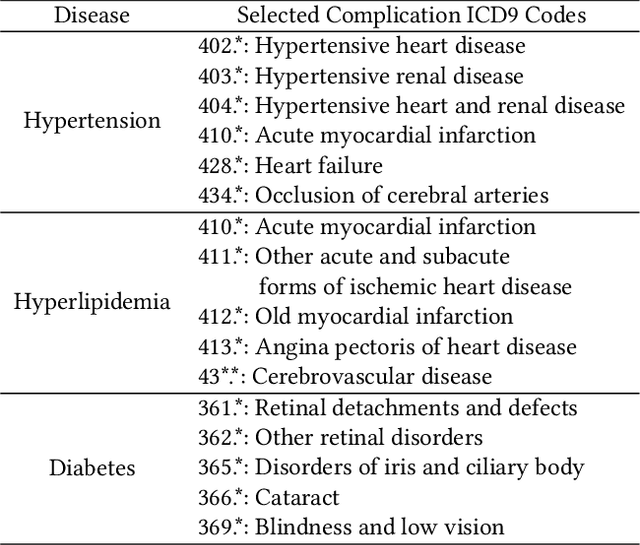
Distance metrics and their nonlinear variant play a crucial role in machine learning based real-world problem solving. We demonstrated how Euclidean and cosine distance measures differ not only theoretically but also in real-world medical application, namely, outcome prediction of drug prescription. Euclidean distance exhibits favorable properties in the local geometry problem. To this regard, Euclidean distance can be applied under short-term disease with low-variation outcome observation. Moreover, when presenting to highly variant chronic disease, it is preferable to use cosine distance. These different geometric properties lead to different submanifolds in the original embedded space, and hence, to different optimizing nonlinear kernel embedding frameworks. We first established the geometric properties that we needed in these frameworks. From these properties interpreted their differences in certain perspectives. Our evaluation on real-world, large-scale electronic health records and embedding space visualization empirically validated our approach.

Cross-Global Attention Graph Kernel Network Prediction of Drug Prescription

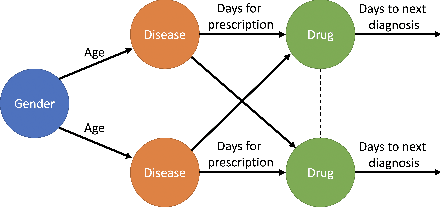
We present an end-to-end, interpretable, deep-learning architecture to learn a graph kernel that predicts the outcome of chronic disease drug prescription. This is achieved through a deep metric learning collaborative with a Support Vector Machine objective using a graphical representation of Electronic Health Records. We formulate the predictive model as a binary graph classification problem with an adaptive learned graph kernel through novel cross-global attention node matching between patient graphs, simultaneously computing on multiple graphs without training pair or triplet generation. Results using the Taiwanese National Health Insurance Research Database demonstrate that our approach outperforms current start-of-the-art models both in terms of accuracy and interpretability.