Solving Parametric PDEs with Radial Basis Functions and Deep Neural Networks

We propose the POD-DNN, a novel algorithm leveraging deep neural networks (DNNs) along with radial basis functions (RBFs) in the context of the proper orthogonal decomposition (POD) reduced basis method (RBM), aimed at approximating the parametric mapping of parametric partial differential equations on irregular domains. The POD-DNN algorithm capitalizes on the low-dimensional characteristics of the solution manifold for parametric equations, alongside the inherent offline-online computational strategy of RBM and DNNs. In numerical experiments, POD-DNN demonstrates significantly accelerated computation speeds during the online phase. Compared to other algorithms that utilize RBF without integrating DNNs, POD-DNN substantially improves the computational speed in the online inference process. Furthermore, under reasonable assumptions, we have rigorously derived upper bounds on the complexity of approximating parametric mappings with POD-DNN, thereby providing a theoretical analysis of the algorithm's empirical performance.

Solving PDEs on Spheres with Physics-Informed Convolutional Neural Networks

Physics-informed neural networks (PINNs) have been demonstrated to be efficient in solving partial differential equations (PDEs) from a variety of experimental perspectives. Some recent studies have also proposed PINN algorithms for PDEs on surfaces, including spheres. However, theoretical understanding of the numerical performance of PINNs, especially PINNs on surfaces or manifolds, is still lacking. In this paper, we establish rigorous analysis of the physics-informed convolutional neural network (PICNN) for solving PDEs on the sphere. By using and improving the latest approximation results of deep convolutional neural networks and spherical harmonic analysis, we prove an upper bound for the approximation error with respect to the Sobolev norm. Subsequently, we integrate this with innovative localization complexity analysis to establish fast convergence rates for PICNN. Our theoretical results are also confirmed and supplemented by our experiments. In light of these findings, we explore potential strategies for circumventing the curse of dimensionality that arises when solving high-dimensional PDEs.

Solving parametric partial differential equations with deep rectified quadratic unit neural networks

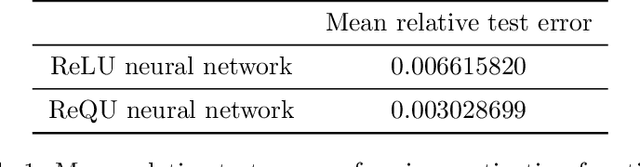
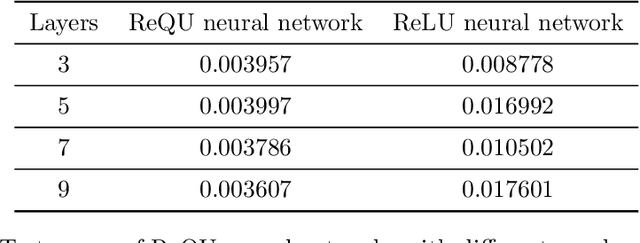
Implementing deep neural networks for learning the solution maps of parametric partial differential equations (PDEs) turns out to be more efficient than using many conventional numerical methods. However, limited theoretical analyses have been conducted on this approach. In this study, we investigate the expressive power of deep rectified quadratic unit (ReQU) neural networks for approximating the solution maps of parametric PDEs. The proposed approach is motivated by the recent important work of G. Kutyniok, P. Petersen, M. Raslan and R. Schneider (Gitta Kutyniok, Philipp Petersen, Mones Raslan, and Reinhold Schneider. A theoretical analysis of deep neural networks and parametric pdes. Constructive Approximation, pages 1-53, 2021), which uses deep rectified linear unit (ReLU) neural networks for solving parametric PDEs. In contrast to the previously established complexity-bound $\mathcal{O}\left(d^3\log_{2}^{q}(1/ \epsilon) \right)$ for ReLU neural networks, we derive an upper bound $\mathcal{O}\left(d^3\log_{2}^{q}\log_{2}(1/ \epsilon) \right)$ on the size of the deep ReQU neural network required to achieve accuracy $\epsilon>0$, where $d$ is the dimension of reduced basis representing the solutions. Our method takes full advantage of the inherent low-dimensionality of the solution manifolds and better approximation performance of deep ReQU neural networks. Numerical experiments are performed to verify our theoretical result.