Eyes-on-Me: Scalable RAG Poisoning through Transferable Attention-Steering Attractors

Existing data poisoning attacks on retrieval-augmented generation (RAG) systems scale poorly because they require costly optimization of poisoned documents for each target phrase. We introduce Eyes-on-Me, a modular attack that decomposes an adversarial document into reusable Attention Attractors and Focus Regions. Attractors are optimized to direct attention to the Focus Region. Attackers can then insert semantic baits for the retriever or malicious instructions for the generator, adapting to new targets at near zero cost. This is achieved by steering a small subset of attention heads that we empirically identify as strongly correlated with attack success. Across 18 end-to-end RAG settings (3 datasets $\times$ 2 retrievers $\times$ 3 generators), Eyes-on-Me raises average attack success rates from 21.9 to 57.8 (+35.9 points, 2.6$\times$ over prior work). A single optimized attractor transfers to unseen black box retrievers and generators without retraining. Our findings establish a scalable paradigm for RAG data poisoning and show that modular, reusable components pose a practical threat to modern AI systems. They also reveal a strong link between attention concentration and model outputs, informing interpretability research.

CmdCaliper: A Semantic-Aware Command-Line Embedding Model and Dataset for Security Research

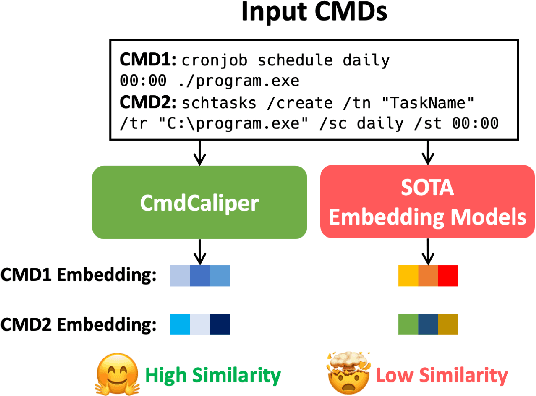
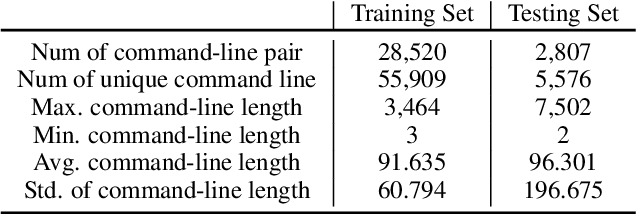
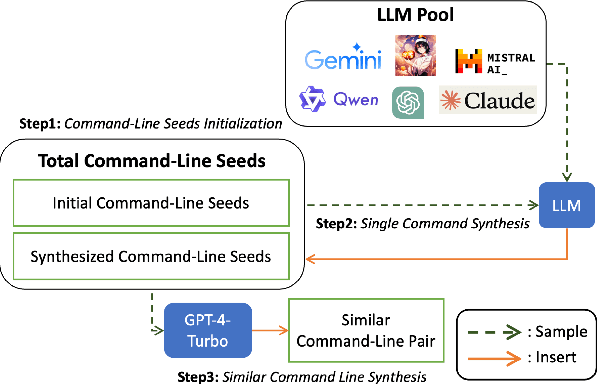
This research addresses command-line embedding in cybersecurity, a field obstructed by the lack of comprehensive datasets due to privacy and regulation concerns. We propose the first dataset of similar command lines, named CyPHER, for training and unbiased evaluation. The training set is generated using a set of large language models (LLMs) comprising 28,520 similar command-line pairs. Our testing dataset consists of 2,807 similar command-line pairs sourced from authentic command-line data. In addition, we propose a command-line embedding model named CmdCaliper, enabling the computation of semantic similarity with command lines. Performance evaluations demonstrate that the smallest version of CmdCaliper (30 million parameters) suppresses state-of-the-art (SOTA) sentence embedding models with ten times more parameters across various tasks (e.g., malicious command-line detection and similar command-line retrieval). Our study explores the feasibility of data generation using LLMs in the cybersecurity domain. Furthermore, we release our proposed command-line dataset, embedding models' weights and all program codes to the public. This advancement paves the way for more effective command-line embedding for future researchers.

With Greater Distance Comes Worse Performance: On the Perspective of Layer Utilization and Model Generalization

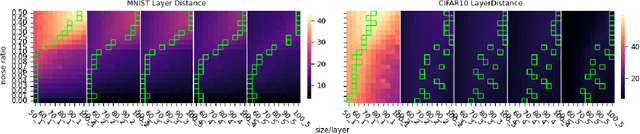
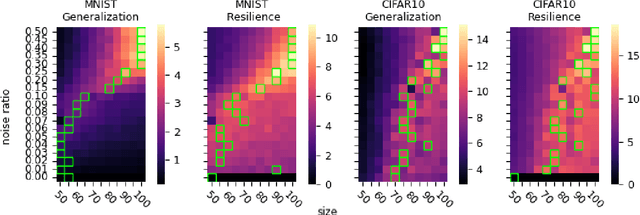
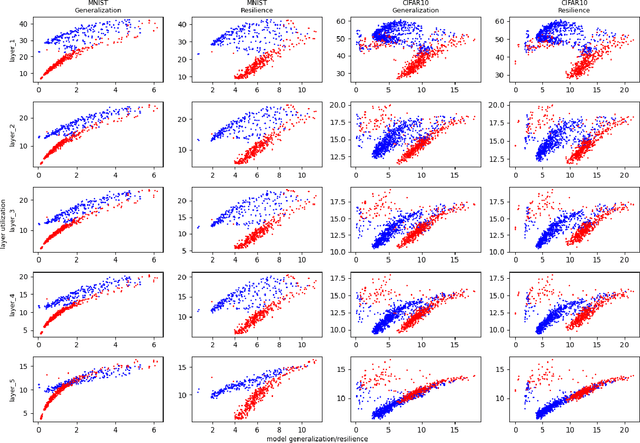
Generalization of deep neural networks remains one of the main open problems in machine learning. Previous theoretical works focused on deriving tight bounds of model complexity, while empirical works revealed that neural networks exhibit double descent with respect to both training sample counts and the neural network size. In this paper, we empirically examined how different layers of neural networks contribute differently to the model; we found that early layers generally learn representations relevant to performance on both training data and testing data. Contrarily, deeper layers only minimize training risks and fail to generalize well with testing or mislabeled data. We further illustrate the distance of trained weights to its initial value of final layers has high correlation to generalization errors and can serve as an indicator of an overfit of model. Moreover, we show evidence to support post-training regularization by re-initializing weights of final layers. Our findings provide an efficient method to estimate the generalization capability of neural networks, and the insight of those quantitative results may inspire derivation to better generalization bounds that take the internal structure of neural networks into consideration.