With Greater Distance Comes Worse Performance: On the Perspective of Layer Utilization and Model Generalization
Paper and Code
Jan 28, 2022
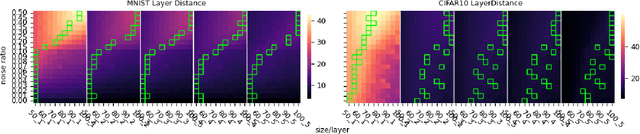
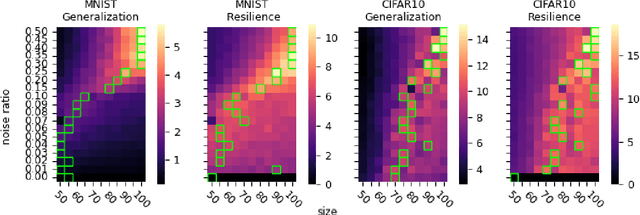
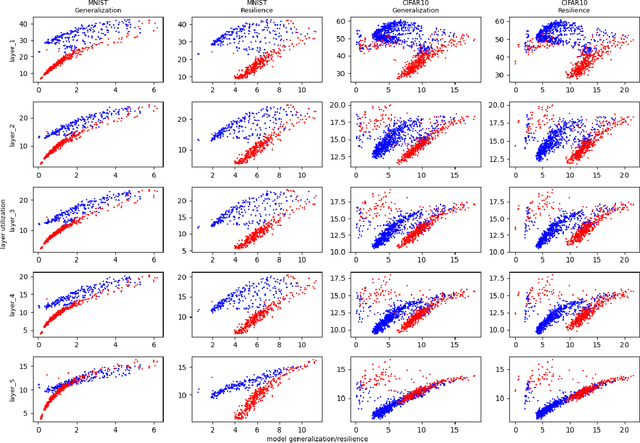
Generalization of deep neural networks remains one of the main open problems in machine learning. Previous theoretical works focused on deriving tight bounds of model complexity, while empirical works revealed that neural networks exhibit double descent with respect to both training sample counts and the neural network size. In this paper, we empirically examined how different layers of neural networks contribute differently to the model; we found that early layers generally learn representations relevant to performance on both training data and testing data. Contrarily, deeper layers only minimize training risks and fail to generalize well with testing or mislabeled data. We further illustrate the distance of trained weights to its initial value of final layers has high correlation to generalization errors and can serve as an indicator of an overfit of model. Moreover, we show evidence to support post-training regularization by re-initializing weights of final layers. Our findings provide an efficient method to estimate the generalization capability of neural networks, and the insight of those quantitative results may inspire derivation to better generalization bounds that take the internal structure of neural networks into consideration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge